Calcul des Courants et Tensions dans un Circuit RLC en Série

Table des Matières

On discute ici de l'utilisation des impédances complexes pour analyser les courants et les tensions dans les circuits RLC en série. Les nombres complexes simplifient grandement les calculs des impédances, des courants et des tensions dans les circuits AC.
Comme le symbole \( i \) est utilisé pour les courants dans les circuits AC, nous utilisons ici \( j \) comme unité imaginaire définie par \( j^2 = -1 \) ou \( j = \sqrt{-1} \)
Les lettres minuscules pour les courants et les tensions sont utilisées pour les quantités réelles. Les lettres majuscules pour les courants et les tensions sont utilisées pour les quantités complexes en forme polaire.

A - Impédances comme Nombres Complexes et Phasors d'un Circuit RLC en Série

Pour un circuit alimenté par une source de tension de fréquence \( f \), les impédances des différents composants RLC sont donnés par :
Les impédances sous forme complexe \( Z_R \) d'une résistance de résistance \( R \) sont données par \[ Z_R = R \] Les impédances sous forme complexe \( Z_L \) d'une inductance d'inductance \( L \), aussi appelée réactance inductive, sont données par \[ Z_L = j \omega L \] Les impédances sous forme complexe \( Z_C \) d'un condensateur de capacité \( C \) , aussi appelée réactance capacitive, sont données par \[ Z_C = - \dfrac{1}{\omega C} j \] où \( \omega = 2 \pi f \)
La chose la plus importante à noter est que les réactances inductive et capacitive dépendent de la fréquence de la source de tension.

Soit \( V_i \), \( I \), \( V_R \), \( V_L \) et \( V_C \) la forme complexe de \( v_i \), \( i \), \( v_R \), \( v_L \) et \( v_C \) respectivement.
Appliquer la loi de Kirchhoff des tensions étendue aux impédances complexes pour écrire
\( V_i - V_R - V_L - V_C = 0\)     (1)
Appliquer la loi d'Ohm étendue aux impédances complexes pour écrire
\( V_R = Z_R I \)
\( V_L = Z_L I \)
\( V_C = Z_C I \)
Substituer ce qui précède dans l'équation (1) pour obtenir
\( V_i = Z_R I + Z_L I + Z_C I = 0\)
Résoudre ce qui précède pour \( I \)
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
Soit \( Z \) l'impédance complexe équivalente du circuit RLC en série définie comme
\[ Z = Z_R + Z_L + Z_C = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
Le module de \( Z \): \[ |Z| = \sqrt{R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \]
L' argument de \( Z \): \[ \theta = arctan \left( \dfrac {\omega L - \dfrac{1}{\omega C}}{R} \right) \]
Notez que tant le module que l'argument de l'impédance \( Z \) dépendent de la fréquence (\( \omega = 2 \pi f \)) de la source de tension. Cette propriété est utile dans la conception de filtres et a de nombreuses autres applications dans les circuits électroniques.
Écrire \( Z \) sous forme polaire
\[ Z = |Z| \; \angle \; \theta \]
Les expressions pour \( Z_R, Z_L, Z_C \) et \( Z \), réalisées ci-dessus, pourraient être interprétées géométriquement en utilisant des phasors comme le montre l'image ci-dessous.


Dans la partie (a), \( Z_R, Z_L\) et \( Z_C \) sont tracés dans un système d'axes avec la partie réelle le long de l'axe horizontal et la partie imaginaire le long de l'axe vertical.
Dans la partie (b), \( Z = Z_R + Z_L + Z_C \) est tracé géométriquement en utilisant l'addition de vecteurs (ou de nombres complexes)
Dans la partie (c), un triangle rectangle avec l'hypoténuse représentant le module de \( Z \) : en utilisant le théorème de Pythagore: \( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \) exactement comme obtenu ci-dessus en utilisant des nombres complexes.
Encore une fois en utilisant le triangle rectangle, l'angle : \( \theta = \arctan \left (\dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)

B - Courant et Tensions d'un circuit RLC en série

Soit \( v_i = V_0 \cos ( \omega t) \), \( V_0 \) le pic de la tension source
Formule d'Euler pour les nombres complexes
\( e^{j \omega t} = \cos (\omega t) + j \sin (\omega t )\)
Ainsi \( v_i \) peut également être écrit comme
\( v_i \) est égal à la partie réelle de \( e^{j \omega t} \)
Nous laissons maintenant tomber la "Partie Réelle de" et effectuons tous les calculs en nombres complexes et définissons \( V_i \) sous forme complexe comme
\( V_i = V_0 e^{j \omega t} \)
et déduisons \( I \) sous forme complexe
\( I = \frac{V_0 e^{j\omega t}}{|Z| \; \angle \; \theta} \)
et \( I \) sous forme polaire est donné par
\( I = \dfrac{V_0}{|Z|} \; \angle \; \omega t - \theta \)
\( I = I_0 \; \angle \; \omega t - \theta \) , où \( I_0 = \dfrac{V_0}{|Z|} \)
Réécrivons les impédances \( Z_R, Z_L\) et \( Z_C \) sous forme polaire
\( Z_R = R = R \; \angle \; 0 \)
\( Z_L = j \omega L = \omega L \; \angle \; \pi/2\)
\( Z_C = - \dfrac{1}{\omega C} j = \dfrac{1}{\omega C} \; \angle \; - \pi/2\ \)
Les tensions sont données par
\( V_R = Z_R I = (R \; \angle \; 0) (I_0 \; \angle \; {\omega t - \theta}) = R I_0 \angle \; \omega t - \theta \)
\( V_L = Z_L I = (\omega L \; \angle \; \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \omega L I_0 \; \angle \; {\omega t - \theta + \pi/2} \)
\( V_C = Z_C I = (\dfrac{1}{\omega C} \; \angle \; - \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \dfrac{I_0}{\omega C} \; \angle \; {\omega t - \theta - \pi/2} \)
Le courant \( I \) et les tensions \( V_R \) , \( V_C \) et \( V_C \) sont représentés ci-dessous à l'aide de phasors.

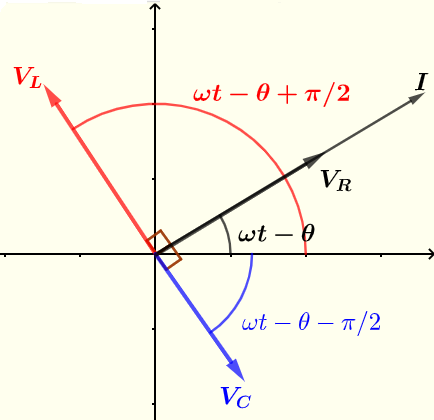
Le courant et les tensions réels sont donnés par la partie réelle de la forme complexe (ou polaire) du courant et des tensions obtenus ci-dessus.
\( i = \dfrac{V_0}{|Z|} \cos( \omega t - \theta) \)

\( v_R = R \dfrac{V_0}{|Z|} \cos(\omega t - \theta) \)

\( v_L = \omega L \dfrac{V_0}{|Z|} \cos(\omega t - \theta + \pi/2) \)

\( v_C = \dfrac{V_0}{\omega C|Z|} \cos(\omega t - \theta - \pi/2) \)

NOTE que la variation temporelle \( \omega t \) peut être omise pendant les calculs et peut être ajoutée à la fin si nous devons écrire les courants et les tensions en fonction du temps. Les exemples ci-dessous montrent comment les circuits RLC sont analysés en ignorant la dépendance temporelle.

C - Exemples avec Solutions Détaillées

Exemple 1
Dans un circuit RLC en série, la tension source est donnée par \( v_i = 20 \cos (\omega t) \), où \( \omega = 1000 \; rad/s \), la capacité du condensateur \( C = 200 \; \mu F \), l'inductance de l'inducteur \( L = 400 \; mH\) et la résistance de la résistance \( R = 400 \; \Omega \).
a) Trouver les impédances du condensateur, de l'inducteur et de la résistance et l'impédance \( Z \) équivalente du circuit RLC sous forme complexe.
b) Trouver le courant et toutes les tensions sous forme complexe.
c) Trouver le courant et les tensions réels.

Solution de l'Exemple 1
a)
Les impédances sous forme complexe \( Z_R \) d'une résistance de résistance \( R \) sont données par
\( Z_R = R = 400 \; \Omega \)
Les impédances sous forme complexe \( Z_L \) d'un inducteur d'inductance \( L \), aussi appelée réactance inductive, sont données par
\( Z_L = j \omega L = j \cdot 1000 \cdot 400 \cdot 10^{-3} = 400 j \; \Omega \)
Les impédances sous forme complexe \( Z_C \) d'un condensateur de capacité \( C \) , aussi appelée réactance capacitive, sont données par
\( Z_C = - \dfrac{1}{\omega C} j = - \dfrac{1}{1000 \cdot 200 \cdot 10^-6} j = - 5 j \; \Omega \)
\( Z = Z_R + Z_L + Z_C = 400 + 400 j - 5 j = 400 + 395 j \)
b)
\( v_i = 20 \cos ( \omega t) \), donc la forme polaire de la tension source \( V_i = 20 \; \angle \; 0\)
Nous avons vu ci-dessus que le courant sous forme polaire est donné par
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
Substituez les quantités connues
\( I = \dfrac{20 \; \angle \; 0}{400 + 395 j}\)
Réécrivez le dénominateur sous forme polaire
\( 400 + 395 j = \sqrt {400^2+395^2} \; \angle \; \arctan\left(\dfrac{395}{400}\right) = 562.16 \; \angle \; 44.64^{\circ} \)
Évaluez \( I \)
\( I = \dfrac{20 \; \angle \; 0}{562.16 \; \angle \; 44.64^{\circ}} = \dfrac{20}{562.16} \; \angle \; 0 - 44.64^{\circ} \)
Simplifiez
\( I = 0.0356 \; \; \angle \; - 44.64^{\circ} \) A
\( V_R = R I = 400 (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; - 44.64^{\circ}\) V
\( V_L = Z_L I = 400 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; 45.36^{\circ}\) V
\( V_C = Z_C I = - 5 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 0.18 \; V \; \angle \; -134.6^{\circ}\) V

Exemple 2
Dans un circuit RLC en série, la tension source est donnée par \( v_i = 10 \cos (\omega t) \), la capacité du condensateur \( C = 200 \; \mu F \), l'inductance de l'inducteur \( L = 200 \; mH\) et la résistance de la résistance \( R = 500 \; \Omega \).
a) Trouver la fréquence angulaire \( \omega \) pour laquelle la partie imaginaire de l'impédance \( Z \) est égale à zéro.
b) Trouver le courant et les tensions pour la fréquence trouvée dans la partie a).

Solution de l'Exemple 2
a)
Pour un circuit RLC en série \( Z = R + j(\omega L - \dfrac{1}{\omega C} ) \)
La partie imaginaire de \( Z \) est égale à zéro donne
\( \omega L - \dfrac{1}{\omega C} = 0 \)
Résolvez pour \( \omega \)
\( \omega^2 L C = 1 \)
\( \omega = \dfrac{1}{\sqrt{L C}} \)
Substituez \( L \) et \( C \) par leurs valeurs numériques
\( \omega = \dfrac{1}{ \sqrt{ 200\cdot10^{-3} \cdot 200 \cdot 10^{-6}}} = 158.11 \) rad/s
b)
\( I = \dfrac{V_i}{Z} = \dfrac{10 \; \angle \; 0}{R \; \angle \; 0} = \dfrac{10}{500} \; \angle \; 0 = 0.02 \; \angle\; 0 \)
\( V_R = R I = 500 \cdot 0.02 \; \angle \; 0 = 10 \; \angle\; 0 \)
\( V_C = Z_C I = \dfrac{1}{\omega C} \; \angle \; -90^{\circ} \cdot 0.02 \; \angle\; 0 = \dfrac{1}{\omega C} \cdot 0.02 \; \angle \; -90^{\circ} = \dfrac{1}{158.11 \cdot 200 \cdot 10^{-6}} \cdot 0.02 \; \angle \; -90^{\circ} = 0.6324 \; \angle \; -90^{\circ} \)
\( V_L = Z_L I = \omega L \; \angle \; 90^{\circ} \cdot 0.02 \; \angle\; 0 = \omega L \cdot 0.02 \; \angle \; 90^{\circ} = 158.11 \cdot 200 10^{-3} \cdot 0.02 \; \angle \; 90^{\circ} = 0.6324 \; \angle \; 90^{\circ} \)

Exemple 3
Dans un circuit RLC en série, la tension source est donnée par \( v_i = V_0 \cos (2 \pi f t) \), où \( f \) est la fréquence, la capacité du condensateur \( C = 47 \; \mu F \), l'inductance de l'inducteur \( L = 100 \; mH\) et la résistance de la résistance \( R = 200 \; \Omega \).
a) Trouver l'impédance totale \( Z \) équivalente au condensateur, à l'inducteur et à la résistance en série en fonction de la fréquence \( f \) et l'écrire sous forme polaire \( Z = |Z| \; \angle \; \theta \)
b) Trouver la fréquence \( f \) telle que \( \theta = -60^{\circ} \).

Solution de l'Exemple 3
a)
Pour un circuit RLC en série \( Z = R + j(\omega L - \dfrac{1}{\omega C}) \)
Substituez les quantités connues par leurs valeurs numériques
\( Z = R + j(\omega L - \dfrac{1}{\omega C}) = 200 + j( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})\)
\( Z = \sqrt {200^2 + ( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})^2} \; \angle \; \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) \)
b)
\( \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) = -60^{\circ} \)
\( \dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200} = \tan (-60^{\circ}) = -1.73205 \)
Multipliez tous les termes de l'équation par \( 200 \) pour éliminer le dénominateur
\( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}} = -346.41 \)
Multipliez tous les termes de l'équation par \( \omega \cdot 47 \cdot 10^{-6} \) pour éliminer le dénominateur
\( 47 \cdot 10^{-7} \omega^2 - 1 = -0.01628127 \omega \)
Résolvez l'équation quadratique ci-dessus pour \( \omega \) et choisissez la solution positive.
\( \omega = 53.23 \) rad/s
\( \omega = 2 \pi f = 60.3682 \)
\( f = \dfrac{60.3682}{2 \pi} = 9.60789 \) Hz

Exemple 4
Dans un circuit RLC en série, la tension source est donnée par \( v_i = V_0 \cos (2 \pi f t) \), la capacité du condensateur \( C = 470 \mu \)F, l'inductance de l'inducteur \( L = 50 \)mH et la résistance de la résistance est \( R \).
a) Trouver l'impédance totale \( Z \) équivalente au condensateur, à l'inducteur et à la résistance en série en fonction de la fréquence \( f \) et l'écrire sous forme polaire \( Z = |Z| \; \angle \; \theta \)
b) Trouver la résistance \( R \) et la fréquence \( f \) telle que \( \theta = 40^{\circ} \) et \( |Z| = 100 \).

Solution de l'Exemple 4
a)
Pour un circuit RLC en série \( Z = R + j(\omega L - \dfrac{1}{\omega C}) \)
Écrivez \( Z \) sous forme polaire
\( Z = \sqrt{R^2 + (\omega L - \dfrac{1}{\omega C})^2} \; \angle \; \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)
b)
\( \theta = \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) = 40^{\circ} \)
\( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} = \tan 40^{\circ} = 0.83909\)
\( \omega L - \dfrac{1}{\omega C} = 0.83909 R \)
Substituez le résultat ci-dessus dans \( |Z| \)
\( \sqrt{R^2 + (0.83909 R)^2} = 100 \)
Résolvez pour \( R \)
\( R = 76.6048 \; \Omega \)
\( \omega L - \dfrac{1}{\omega C} = 0.83909 R = 64.27832 \)
Résolvez pour \( \omega \)
\( \omega = 1317.8557 \) rad/s
\( f = \dfrac{1317.8557}{2\pi} = 209.74324 \) Hz

Plus de Références et Liens