Utilisation des nombres complexes dans les circuits en CA

Table des matières

Il est ici discuté comment les nombres complexes peuvent être utilisés pour analyser et calculer les courants et les tensions dans les circuits en CA (courant alternatif) et aussi comment la résistance, l'impédance d'un condensateur et l'impédance d'une bobine sont représentées par des nombres complexes. Il est également montré comment l'utilisation d'impédances complexes permet l'utilisation d'une loi similaire à la loi d'Ohm pour modéliser mathématiquement les circuits en CA.
Deux principales raisons qui rendent l'utilisation des nombres complexes appropriée pour modéliser les circuits en CA, et de nombreux autres phénomènes de sinusoïde dans plusieurs branches de l'ingénierie, sont :
1) les signaux en CA (et de nombreux autres phénomènes de sinusoïde) sont caractérisés par une magnitude et une phase qui sont, respectivement, très similaires au module et à l'argument des nombres complexes.
2) les opérations de base telles que l'addition, la soustraction, la multiplication et la division des nombres complexes sont plus faciles à effectuer et à programmer sur un ordinateur.
Remarque
1) Parce que le symbole \( i \) est utilisé pour les courants dans les circuits en CA, ici nous utilisons \( j \) comme l'unité imaginaire définie par \( j^2 = -1 \) ou \( j = \sqrt{-1} \)
2) Le symbole \( \Re e\) représente la partie réelle d'un nombre complexe.

A - Partie Réelle des Nombres Complexes

Un nombre complexe en forme standard \( Z = a + j b \) peut être écrit sous forme exponentielle comme suit
\( \displaystyle Z = r e^{j \theta} \)      avec \( j^2 = -1 \)
et en forme polaire comme suit
\( Z = r \angle \theta \)
où \( r = \sqrt{a^2 +b^2} \) est le module de \( Z \) et \( \tan \theta = \dfrac{b}{a} \) son argument.
Prenez la partie réelle, écrite comme \( \Re e \), de chaque côté d'un nombre complexe en forme exponentielle
\( \Re e (r e^{j \theta}) = \Re e (r ( \cos \theta + j \sin \theta )) = \Re e (r \cos \theta + j r \sin \theta ) = r \cos \theta \)
Dans ce qui suit, \( \Re e \) signifie la partie réelle d'un nombre complexe donné.

B - Dérivée des Fonctions Complexes avec une Variable

Soit \( f(t) \) une fonction complexe avec une variable \( t \) qui est écrite sous la forme
\( f(t) = a(t) + j b(t) \)
où \( a(t) \) est la partie réelle de \( f(t) \), \( b(t) \) est la partie imaginaire de \( f(t) \) et \( j = \sqrt {-1}\) est l'unité imaginaire.
Soit \( f'(t) \) la première dérivée de \( f(t) \) par rapport à \( t \) définie par
\( f'(t) = \lim_{h\to 0} \dfrac{f(t+h) - f(t) }{h} \)
Remplacez \( f(t+h) \) par \( a(t+h) + j b(t+h) \) dans la formule ci-dessus.
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) + j b(t+h) - (a(t) + jb(t))}{h} \)
Séparez les termes comme suit
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) - a(t)}{h} + j \lim_{h\to 0} \dfrac{ j b(t+h) - jb(t))}{h} \)
\( f'(t) = a'(t) + j b'(t) \)
Il est maintenant facile de montrer que la partie réelle de la dériv ée de \( f(t) \) est égale à la dérivée de la partie réelle de \( f(t) \) ce qui peut s'écrire comme
\( \Re e(f'(t)) = a'(t) = (\Re e(f(t))' \)
ou
\( \Re e \left ( \dfrac{df(t)}{dt} \right) = \dfrac {d a(t)}{dt} = \dfrac {d \left (\Re e(f(t)) \right)}{dt} \)

C - Intégrale des Fonctions Complexes avec une Variable

Soit \( f(t) \) une fonction complexe avec une variable \( t \) qui est écrite sous la forme
\( f(t) = a(t) + j b(t) \)
où \( a(t) \) est la partie réelle de \( f(t) \), \( b(t) \) est la partie imaginaire de \( f(t) \) et \( j = \sqrt {-1}\) est l'unité imaginaire.
Soit \( F(t) \) défini par l'intégrale indéfinie
\( \displaystyle F(t) = \int f(t) dt = \int (a(t) + j b(t)) dt = \int a(t) dt + j \int b(t) dt \)
Il est maintenant facile de montrer que la partie réelle de l'intégrale de \( f(t) \) est égale à l'intégrale de la partie réelle de \( f(t) \) ce qui peut s'écrire comme
\( \displaystyle \Re e \left( \int f(t) dt \right) = \int a(t) dt = \int \left( \Re e f(t) \right) dt \)

Nous utilisons maintenant les concepts ci-dessus pour analyser des circuits en CA simples en utilisant des nombres complexes.

D - Source de Tension en CA et Nombres Complexes

Dans ce qui suit, \( v(t) \) est une source de tension en CA, qui varie avec le temps \( t \), donnée par
\( v(t) = V_0 \cos(\omega t) \)
où \( V_0 \) est un nombre réel égal à la tension de crête et \( \omega = 2 \pi f \) est également un nombre réel avec \( f \) la fréquence de la source de tension.
En utilisant les nombres complexes, \( v(t) \) peut également être écrit comme
\( v(t) = V_0 \cos(\omega t) = \Re e ( V_0 \cos(\omega t) + j V_0 \sin(\omega t) ) = \Re e (V_0 e^{j\omega t} ) \)

E - Résistance dans un circuit en CA

Considérons un circuit en CA simple avec une résistance comme illustré ci-dessous. Soit \( v(t) \) une source de tension en CA donnée par
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
où \( V_0 \) et \( \omega \) sont des quantités réelles.


La relation entre le courant \( i \) à travers et la tension \( v(t)_R \) aux bornes de la résistance \( R \) est donnée par
\( v(t)_R = R i \)
En utilisant la seule boucle montrée ci-dessus, nous avons
\( v(t) = v(t)_R \)
\( v(t) \) est donné par \( v(t) = V_0 \cos(\omega t) \)
d'où
\( v(t)_R = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
en combinant ce qui précède, nous écrivons
\( R i = \Re e (V_0 e^{j\omega t} ) \)       (I)
Soit \( V_R = V_0 e^{j\omega t} \) et réécrivons (I) ci-dessus comme
\( R i = \Re e V_R \)
puisque \( R \) est une quantité réelle, ce qui précède peut être écrit comme
\( i = \Re e \left( \dfrac{V_R }{R} \right) \)
Soit \( Z_R \) défini comme l'impédance d'une résistance telle que
\( Z_R = R \)
Puisque \( R \) est réel, l'impédance \( Z_R \) d'une résistance est un nombre réel.
Le courant \( i \) peut alors être écrit comme
\( i = \Re e \left( \dfrac{ V_R } {Z_R} \right) \)
Soit
\( I = \dfrac{ V_R } {Z_R} \)
Ce qui donne une relation similaire à la loi d'Ohm dans les circuits en courant continu (CC). La relation ci-dessus entre les grandeurs complexes \( I \), \( V_R \) et \( R \) facilite beaucoup les calculs.
Cela simplifie les calculs dans le sens où nous effectuons des calculs en utilisant des impédances complexes, des tensions et des courants, puis prenons la partie réelle comme réponse finale.

F - Condensateur dans un circuit en CA

Considérons un circuit en CA simple avec un condensateur comme illustré ci-dessous. Soit \( v(t) \) une source de tension en CA donnée par
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

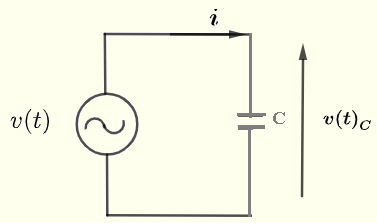
La relation entre le courant \( i \) à travers et la tension \( v(t)_C \) aux bornes du condensateur \( C \) est donnée par
\( \displaystyle v(t)_C = \dfrac{1}{C} \int i dt \)
En utilisant la seule boucle montrée ci-dessus, nous avons
\( v(t) = v(t)_C \)
Étant donné
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
nous combinons tout ce qui précède pour écrire
\( \displaystyle \Re e (V_0 e^{j\omega t} ) = \dfrac{1}{C} \int i dt \)
Nous prenons la dérivée des deux côtés
\( \displaystyle \dfrac{d}{dt} (\Re e (V_0 e^{j\omega t}) ) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
Utilisant le résultat déjà discuté dans la partie C ci-dessus, nous réécrivons ce qui précède comme
\( \displaystyle \Re e \dfrac{d}{dt} \left( V_0 e^{j\omega t} \right) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
Simplifions
\( \Re e \left( j \omega V_0 e^{j\omega t} \right) = \dfrac{1}{C} i \)
Puisque la capacité \( C \) est une quantité réelle, nous pouvons écrire
\( i = \Re e \left( j \omega C \; V_0 e^{j\omega t} \right) \)
Soit \( V_C = V_0 e^{j\omega t} \) et définissons \( Z_C \) comme l'impédance complexe d'un condensateur tel que
\( Z_C = \dfrac{1}{j \omega C} = - \dfrac {j} { \omega C} \)
Puisque \( C \) est réel, l'impédance \( Z_C \) d'un condensateur est un nombre imaginaire pur.
Le courant \( i \) peut alors être écrit comme
\( i = \Re e \left( \dfrac{ V_C } {Z_C} \right) \)
Soit
\( I = \dfrac{ V_C } {Z_C} \)
Ce qui est similaire à la loi d'Ohm dans les circuits en courant continu (CC). La relation ci-dessus entre les grandeurs complexes \( I \), \( V_C \) et \( Z_C \) facilite beaucoup les calculs.
Cela simplifie les calculs dans le sens où nous effectuons des calculs en utilisant des impédances complexes, des tensions et des courants, puis prenons la partie réelle comme réponse finale.

G - Inducteur dans un circuit en CA

Considérons un circuit en CA simple avec un condensateur comme illustré ci-dessous. Soit \( v(t) \) une source de tension en CA donnée par
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

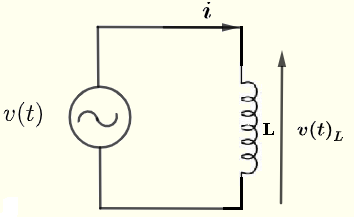
La relation entre le courant \( i \) à travers et la tension \( v(t)_L \) aux bornes de l'inducteur avec une inductance \( L \) est donnée par
\( v(t)_L = L \dfrac {d i}{ dt} \)
En utilisant la seule boucle montrée ci-dessus, nous avons
\( v(t) = v(t)_L \)
Étant donné
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
nous combinons tout ce qui précède pour écrire
\( \Re e (V_0 e^{j\omega t} ) = L \dfrac {d i}{ dt} \)
Prenons l'intégrale indéfinie des deux côtés
\( \displaystyle \int \Re e (V_0 e^{j\omega t}) dt = \int L \dfrac {d i}{ dt} dt \)
Utilisons le résultat déjà discuté dans la partie C ci-dessus, nous réécrivons ce qui précède comme
\( \displaystyle \Re e \int V_0 e^{j\omega t} dt = \int L \dfrac {d i}{ dt} dt \)
Calculons les intégrales des deux côtés
\( \Re e \left( \dfrac{1}{j\omega} V_0 e^{j\omega t} \right) = L i \)
Puisque l'inductance \( L \) est une quantité réelle, nous pouvons écrire
\( i = \Re e \left( \dfrac{1}{j \omega L} \; V_0 e^{j\omega t} \right) \)
Soit \( V_L = V_0 e^{j\omega t} \) et \( Z_L \) soit défini comme l'impédance d'un inducteur tel que
\( Z_L = j \omega L \)
Puisque \( L \) est réel, l'impédance \( Z_L \) d'un condensateur est un nombre imaginaire pur.
Le courant \( i \) peut alors être écrit comme
\( i = \Re e \left( \dfrac{ V_L } {Z_L} \right) \)
Soit
\( I = \dfrac{ V_L } {Z_L} \)
Ce qui donne une relation similaire à la loi d'Ohm entre les grandeurs complexes \( I \), \( V_L \) et \( Z_L \).
Cela simplifie les calculs dans le sens où nous effectuons des calculs en utilisant l'impédance complexe, la tension et le courant, puis prenons la partie réelle comme réponse finale.

H - Conclusion : Loi d'Ohm avec des Impédances Complexes

Nous avons vu ci-dessus que les impédances des résistances, des condensateurs et des inductances peuvent être définies comme des quantités complexes qui peuvent être soit purement réelles, soit purement imaginaires, données par
1) Pour une résistance \( R\) ; l'impédance est donnée par \[ Z_R = R \] et la relation entre le courant \( I \) (sous forme complexe) à travers et la tension \( V_R \) (sous forme complexe) aux bornes de la résistance \( R \) est la loi d'Ohm en CA et est donnée par : \[ I = \dfrac{V_R}{Z_R} \] 2) Pour un condensateur \( C \) ; l'impédance est donnée par \[ Z_C = -\dfrac{j}{\omega C} \] et la relation entre le courant \( I \) (sous forme complexe) à travers et la tension \( V_C \) (sous forme complexe) aux bornes du condensateur \( C \) est la loi d'Ohm en CA et est donnée par : \[ I = \dfrac{V_C}{Z_C} \] 3) Pour une inductance \( L \) ; l'impédance est donnée par \[ Z_L = j \omega L \] et la relation entre le courant \( I \) (sous forme complexe) à travers et la tension \( V_L \) (sous forme complexe) aux bornes de l'inducteur \( L \) est la loi d'Ohm en CA et est donnée par : \[ I = \dfrac{V_C}{Z_L} \] Nous concluons que la loi d'Ohm est valide dans les circuits en CA lorsque des nombres complexes sont utilisés pour modéliser les impédances des résistances, des condensateurs et des inductances.
Il peut également être démontré que les lois de Kirchhoff sont également valides dans les circuits en CA lorsque des nombres complexes sont utilisés pour modéliser les impédances des résistances, des condensateurs et des inductances.
Les impédances équivalentes aux impédances en série et en parallèle peuvent être calculées en utilisant des règles similaires pour les résistances en série et en parallèle.

E - Exemples avec Solutions

Exemple 1
Trouver le courant \( i \), la tension \( v(t)_R \) aux bornes de la résistance \( R \) et la tension \( v(t)_L \) aux bornes de l'inductance \( L \) en termes de \( V_0 \), \( R \), \( L \) et \( \omega \) étant donné
la source de tension : \( v(t) = V_0 \cos(\omega t) \) , \( \omega = 2 \pi f \) et \( f \) est la fréquence.

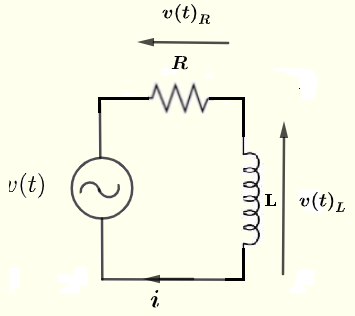
Solution à l'Exemple 1
Soit \( V \) la forme complexe de la source de tension \( v(t) \).
Soit \( V_R \) la forme complexe de la tension \( v(t)_R\) aux bornes de la résistance R.
Soit \( V_L \) la forme complexe de la tension \( v(t)_L\) aux bornes de l'inductance L
Soit \( I \) la forme complexe du courant \( i \) à travers la résistance et le condensateur dans le circuit donné.
Soit l'impédance complexe d'une résistance \( Z_R = R \) et celle de l'inductance \( Z_L = j \omega L \) (voir partie H ci-dessus).
Redessinez le circuit avec les quantités complexes définies ci-dessus et vous pouvez appliquer les lois d'Ohm et de Kirchhoff.

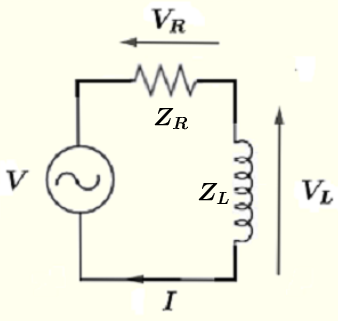
En utilisant la loi de Kirchhoff sur la boucle formant le circuit, nous avons
\( V = V_R + V_L \)         (I)
En utilisant la loi d'Ohm pour réécrire \( V_R \) et \( V_L \) comme
\( V_R = Z_R I \)
\( V_L = Z_L I \)
Substituer dans l'équation (I)
\( V = Z_R I + Z_L I = R I + j \omega L I = I(R + j \omega L ) \)
Résoudre ce qui précède pour \( I \)
\( I = \dfrac{V}{R+j \omega L} \)         (II)
Le dénominateur \( R+j \omega L \) est un nombre complexe qui peut être écrit sous forme complexe comme
\( R+j \omega L = r e^{j\theta} \)
où
\( r = |Z| = \sqrt {R^2 + (L\omega)^2} \) est le module
\( \theta = \arctan \left(\dfrac{\omega L}{R} \right) \) est l'argument comme indiqué dans le plan complexe ci-dessous.

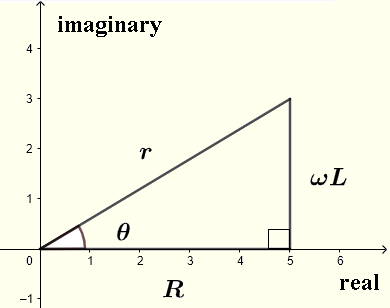
Soit \( V = V_0 e^{j\omega t} \)
Substituer \( V \) et \( R+j \omega L \) par leurs formes complexes dans (II) et écrire
\( I = \dfrac{V_0 e^{j\omega t}}{r e^{j\theta}} \)
Utiliser les règles exponentielles pour simplifier ce qui précède
\( I = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Utiliser la loi d'Ohm pour écrire
\( V_R = R I = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)

\( V_L = Z_L I = \dfrac{j V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Écrire \( j \) sous forme exponentielle \( j = e^{j \pi/2} \) dans \( V_L \)
\( V_L = \dfrac{ e^{j \pi/2} V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Utiliser la règle exponentielle pour réécrire ce qui précède comme
\( V_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \)
Nous utilisons maintenant les quantités complexes calculées ci-dessus pour calculer \( i \), \( v(t)_R \) et \( v(t)_L \) en prenant les parties réelles comme suit :
\( i = \Re e I = \Re e \left( \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \)
ce qui donne
\[ i = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_R = \Re e V_R = \Re e \left( \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \) \[ v(t)_R = \ dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_L = \Re e V_L = \Re e \left( \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \right) \) \[ v(t)_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t + \pi/2 -\theta) \]

Plus de Références et Liens