多变量函数的定义及其定义域的概念通过示例进行了说明。
问题及其解决方案也包含在内。
在找到二元函数的定义域时,需要掌握解决二元不等式系统的技能。
让我们考虑一些非常著名的公式。
a) 边长为 \( x \) 的正方形的周长 \( P \) 表示为 \( P = 4 x\)。
b) 长为 \( L \)、宽为 \( W \) 的矩形的面积 \( A \) 表示为 \( A = L W \)
c) 根据牛顿万有引力定律,两物体质量分别为 \( m_1 \) 和 \( m_2 \) 且相距 \( d \) 的力 \( F \) 表示为 \( F = G \dfrac{m_1 m_2}{d^2} \)
其中 \( G \) 是一个常数。
可以说:
a) 中的周长 \( P \) 是一个单变量函数 \( x \)
b) 中的面积 \( A \) 是一个二元函数 \( L \) 和 \( W \)
c) 中的力 \( F \) 是一个三元函数 \( m_1 \)、\( m_2 \) 和 \( d \) (注意:\( G \) 是一个常数)。
一个函数 \( f \) 有 \( n \) 个变量 \( x_1, x_2, ...., x_n \),它是一个规则,该规则将唯一的实数 \( f (x_1, x_2, ...., x_n) \) 分配给每个 n 元组的实数 \( x_1, x_2, ...., x_n \)。
对于函数 \( f \) 唯一取实数值的所有 n 元组 \( x_1, x_2, ...., x_n \) 组成的集合 \( D \) 称为函数 \( f \) 的定义域。
如果我们令 \( u = f (x_1, x_2, ...., x_n) \),对应于所有 n 元组 \( x_1, x_2, ...., x_n \) 的 \( u \) 的所有值的集合称为 \( f \) 的值域 [1] , [2] , [3] 。
例 1 二元函数
给定函数 \( f \) ,定义为
\[ f(x,y) = \sqrt{x^2+y^2} + \ln(x-y) \]
a) 计算: \( f(4,3) \) , \( f(e^2,0) \)
b) 找到并绘制函数 \( f \) 的定义域
例 1 解答
a)
计算 \( f(4,3) \) 时,需要将 \( x \) 替换为 \( 4 \),将 \( y \) 替换为 \( 3 \)
因此
\( f(4,3) = \sqrt{4^2+3^2} + \ln(4-3) \)
简化
\( \quad = \sqrt{25} + \ln(1) = 5 + 0 = 5 \)
计算 \( f(e^2,0) \) 时,需要将 \( x \) 替换为 \( e^2 \),将 \( y \) 替换为 \( 0 \)
因此
\( f(e^2,0) = \sqrt{e^2 + 0^2} + \ln(e^2 - 0) \)
简化
\( \quad = e + 2 \)
b)
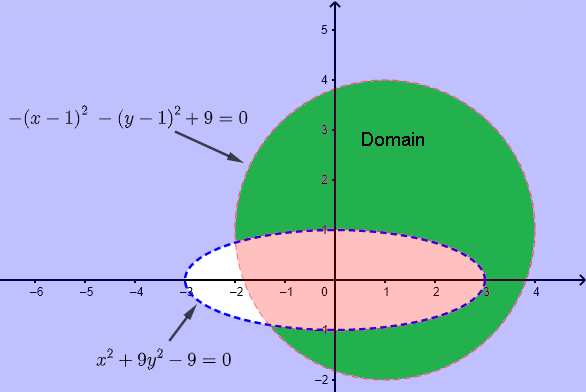
函数 \( f(x,y) \) 的定义域通过设置以下条件来找到:
1) \( \quad x^2+y^2 \ge 0 \),平方根下的值必须为非负数
2) \( \quad x - y \gt 0 \),对数的自变量必须为正数。
上述条件 1) 总是满足的。
条件 2) 的不等式可以通过图形解决,得到如下图所示的解。

例 2 三元函数
给定函数 \( g \),定义为
\[ g(x,y,z) = \sqrt{ x^2 + y^2 + z^2 - 9} \]
a) 计算:\( g(3,-1,1) \) , \( g(3/2,1/4,7/2) \)
b) 找到并描述函数 \( g \) 的定义域
例 2 解答
a)
计算 \( g(3,-1,1) \) 时,需要将 \( x \) 替换为 \( 3 \),将 \( y \) 替换为 \( -1 \),将 \( z \) 替换为 \( 1 \)
因此
\( g(3,-1,1) = \sqrt{ 3^2 + (-1)^2 + 1^2 - 9} \)
简化
\( \quad = \sqrt{2} \)
计算 \( g(3/2,1/4,7/2) \) 时,需要将 \( x \) 替换为 \( 3/2 \),将 \( y \) 替换为 \( 1/4 \),将 \( z \) 替换为 \( 7/2 \)
因此
\( g(3/2,1/4,2) = \sqrt{ (3/2)^2 + (1/4)^2 + (7/2)^2 - 9} \)
简化
\( \quad = \dfrac{\sqrt{89}}{4} \)
b)
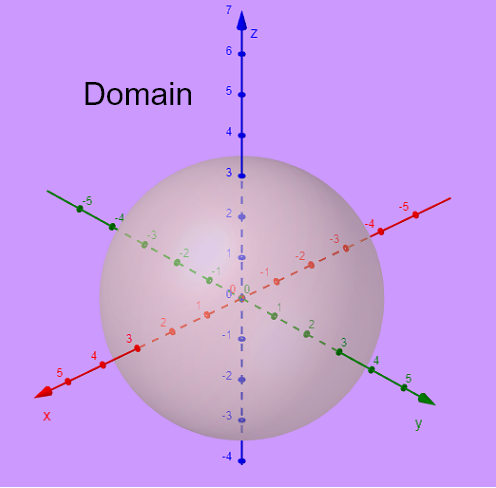
函数 \( g(x,y,z) \) 的定义域通过设置以下条件来找到:
\( x^2 + y^2 + z^2 - 9 \ge 0 \) ,平方根下的值必须为非负数
考虑 \( x^2 + y^2 + z^2 - 9 = 0 \) ,它可以写为 \( x^2 + y^2 + z^2 = 3^2 \)。
因此,方程 \( x^2 + y^2 + z^2 - 9 = 0 \) 的图形是一个以原点 \( (0,0,0) \) 为中心、半径为 \( 3 \) 的球体,如下图所示。
例 3 二元函数
给定函数 \( h \),定义为
\[ h(x,y) = \dfrac{1}{\ln (1 - x y) } - \sqrt{x - y^2}\]
a) 找到并描述函数 \( h \) 的定义域
b) 给出 3 组位于函数 \( h \) 定义域中的有序对 \( (x,y) \) 的示例,并在这些点上计算函数值。
c) 给出 3 组不在定义域中的有序对 \( (x,y) \) 的示例。
例 3 解答
a)
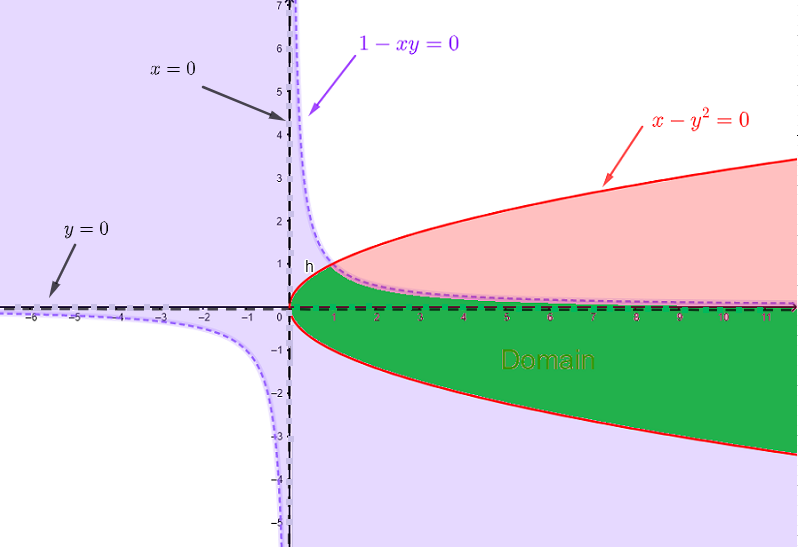
函数 \( h(x,y) \) 的定义域通过设置以下条件来找到:
1) \( \quad 1 - x y \gt 0 \) ,对数的自变量必须为正数
2) \( \quad x - y^2 \ge 0 \) ,平方根下的值必须为非负数。
3) \( \quad \ln (1 - x y) \ne 0 \) 或 \( 1 - xy \ne 1 \),这等效于 \( xy \ne 0 \),分母 \( \ln (1 - x y) \) 不能为零。
条件 1) 通过绘制 \( 1 - x y = 0 \) 的图形来解决,这等效于 \( y = \dfrac{1}{x} \),并选择满足不等式 \( \quad 1 - x y \gt 0 \) 的解集。(浅紫色区域)
条件 2) 通过绘制 \( x - y^2 = 0 \) 的图形来解决,这等效于 \( x = y^2 \),这是一个水平抛物线,并选择满足不等式 \( \quad x - y^2 \ge 0 \) 的解集。(红色区域)
条件 3) 通过排除位于任一坐标轴上的点来满足。(虚线)
定义域是条件 1)、2) 和 3) 中找到的所有解集的交集,如下图所示(绿色区域),排除任何位于 \( x \) 轴或 \( y \) 轴上的点。
A 部分
给定函数:
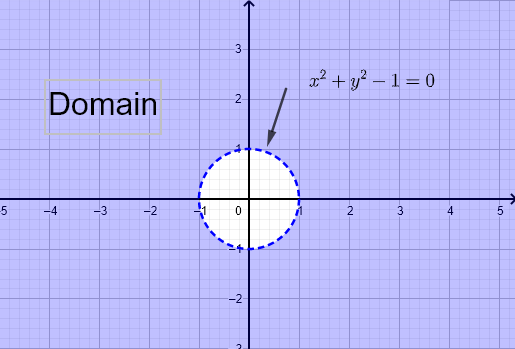
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) 和 \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a) 找到每个函数的定义域
b) 计算
1) \( f (1,0) \) , 2) \( g (1,-1) \) , 3) \( \dfrac{f(3,4)}{g(2,0)} \)
B 部分
在一个电路中,三个并联电阻的总电阻 \( R \) 与各电阻 \( r_1 , r_2 , r_3 \) 的关系为
\( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \)
a) 将 \( R \) 表示为 \( r_1 , r_2 , r_3 \) 的函数。
b) 计算当 \( r_1 = 100 \),\( r_2 = 50 \) 和 \( r_3 = 20 \) 时的 \( R \)。
C 部分
找到函数的定义域
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
b) \( h(x,y) = \dfrac{\ln(x^2+9 y^2-9)}{\sqrt{7-x^2-y^2+2 x + 2 y}} \)
A 部分
\( f (x,y) = \dfrac{1}{\sqrt{x^2 - y}} \) 和 \( g (x,y) = \ln (x^2 + y^2 - 1) \)
a)
函数 \( f \) 的定义域通过解 \( x^2 - y \gt 0 \) 来找到;分母不能为零,且平方根的自变量必须为非负数。
绘制 \( y = x^2 \) 的图形,并选择满足不等式 \( x^2 - y \gt 0 \) 的区域。图形解如下所示。定义域是抛物线 \( y = x^2 \) 外部的所有点 \( (x,y) \) 的集合。

B 部分
a)
给定 \( \dfrac{1}{R} = \dfrac{1}{r_1} + \dfrac{1}{r_2} + \dfrac{1}{r_3} \),
将方程的所有项乘以 \( r_1 r_2 r_3 \) 的乘积
\( \dfrac{r_1 r_2 r_3}{R} = \dfrac{r_1 r_2 r_3}{r_1} + \dfrac{r_1 r_2 r_3}{r_2} + \dfrac{r_1 r_2 r_3}{r_3} \)
简化
\( \dfrac{r_1 r_2 r_3}{R} = r_2 r_3 + r_1 r_3 + r_1 r_2 \)
求解 \( R \)
\( R(r_1,r_2,r_3) = \dfrac{r_1 r_2 r_3}{r_2 r_3 + r_1 r_3 + r_1 r_2} \)
b)
\( R(100,50,20) = \dfrac{100 \times 50 \times 20}{50 \times 20 + 100 \times 20 + 100 \times 50} = 12.5\)
C 部分
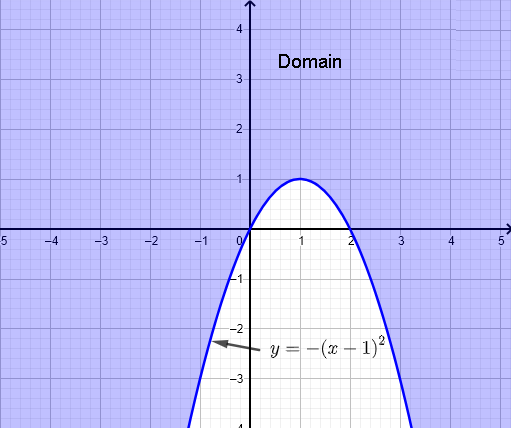
a) \( f(x,y) = \sqrt{x^2+y-2x} \)
\( f(x,y) \) 取实数值的条件是平方根的自变量非负数,因此要求
\( x^2+y-2x \ge 0 \)
完成平方并重写为
\( (x-1)^2 - 1 + y \ge 0 \)
\( y \ge - (x-1)^2 + 1 \)
绘制抛物线 \( y = - (x-1)^2 + 1 \),并确定函数 \( f \) 的定义域。
定义域是抛物线 \( y = - (x-1)^2 + 1 \) 上或外部的点 \( (x,y) \) 的集合,如下图所示(紫色区域)。