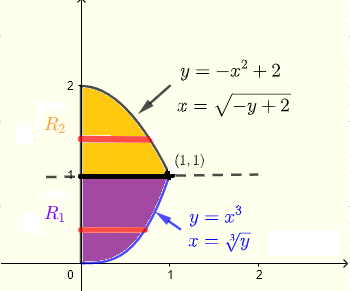一般区域上的二重积分

本文提供了一些在一般区域上计算和评估二重积分的示例，并附有详细的解答。
重要说明
1) 在一般的非矩形区域上绘制图形和示意图作为第一步，可以使计算二重积分更加容易。
2) 一般来说，计算一般积分区域上的二重积分需要四个步骤：
步骤 1：绘制积分区域的图形和/或示意图
步骤 2：决定如何使用垂直或水平条带来描述一般区域，并因此确定积分的顺序
步骤 3：使用不等式描述积分区域
步骤 4：计算积分
3) 在接下来的内容中，我们将积分区域 \( R \) 描述为无限的垂直条带集合，这样积分可以表示为 \( \displaystyle \iint_R f(x,y) \;dy \;dx \) 或水平条带集合，这样积分可以表示为 \( \displaystyle \iint_R f(x,y) \;dx \;dy \) \( \)\( \)\( \)

一般区域上的二重积分的计算

示例 1 和 2 的目标是使用图形和示意图来确定一般区域的积分限并计算二重积分。

示例 1
问题：计算二重积分 \( \displaystyle V = \iint_R (x^2+y) \;dy \;dx \)，其中区域 \( R \) 是由 \(x\)-轴、\(y\)-轴和直线 \( y = - x + 2 \) 围成的三角形。
示例 1 的解答
计算一般积分区域上的二重积分需要四个主要步骤。
步骤 1 绘制表示一般区域的图形和/或示意图
我们首先通过绘制积分区域 \( R \) 的图形或示意图开始。在这个例子中，它是一个三角形，其边在 \(x\) 轴和 \(y\) 轴上，第三边由直线 \( y = - x + 2 \) 表示。这个三角形也可以通过三个顶点定义：原点和直线 \( y = - x + 2 \) 与 \(x\) 轴和 \(y\) 轴的交点，分别是 \( (2,0) \) 和 \( (0,2) \)，如下面的图形所示。

示例 1 的三角形区域

计算给定区域上的积分有两种方法。
步骤 2 决定如何使用条带描述一般区域
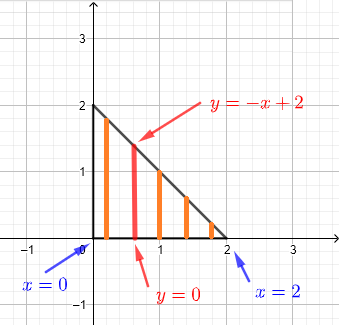
1) 我们使用垂直条带来描述区域 \( R \)，如下面的图所示。
我们假设区域 R 可以被认为是无限的垂直条带集合，如下图所示。
在给定 \( x \) 处的任意垂直条带从 \( y = 0 \) 开始，到 \( y = - x + 2 \) 结束。由于我们必须包括描述区域 \( R \) 的所有条带，因此 \( x \) 必须取值从 \( x = 0 \) 到 \( x = 2 \)。因此，积分区域 \( R \) 可以定义为：
步骤 3 使用不等式描述积分区域
\( R \) ：\( 0 \le x \le 2 \) , \( 0 \le y \le - x + 2 \)
垂直条带描述的区域

步骤 4 计算积分
积分可以写为：
\( \displaystyle V = \int_0^2 \int_0^{-x+2} (x^2+y) \;dy \;dx \)
\( = \displaystyle \int_0^2 (-x^3 +\dfrac{5}{2} x^2 - 2x + 2) \;dx = 8/3\)

现在我们使用水平条带回答相同的问题。步骤 1 同上
步骤 2 决定如何使用条带描述一般区域
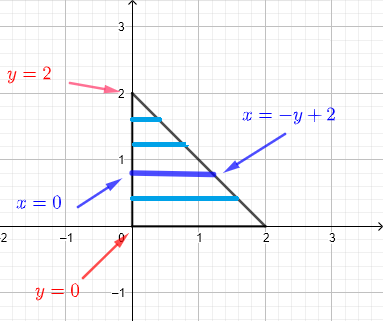
2) 我们使用水平条带来描述区域 \( R \)，如下面的图所示。
我们假设区域 R 可以被认为是无限的水平条带集合，如下图所示。
在给定 \( y \) 处的任意水平条带从 \( x = 0 \) 开始，到 \( x = - y + 2 \) 结束。由于我们必须包括所有描述区域 \( R \) 的条带，因此 \( y \) 必须取值从 \( y = 0 \) 到 \( y = 2 \)。因此，积分区域 \( R \) 可以定义为：
步骤 3 使用不等式描述积分区域
\( R \) ：\( 0 \le x \le - y + 2 \) , \( 0 \le y \le 2 \)

水平条带描述的区域

步骤 4 计算积分
因此，积分可以写为：
\( \displaystyle V = \int_0^2 \int_0^{-y+2} (x^2+y) \;dx \;dy \)
\( = \displaystyle \int_0^2 (-\dfrac{1}{3} y^3 + y^2 - 2 y + \dfrac{8}{3}) \;dy = 8/3 \)
注意在两种情况下，包含变量的积分限都是内积分

示例 2
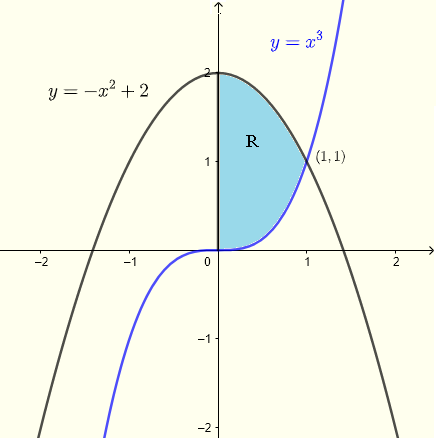
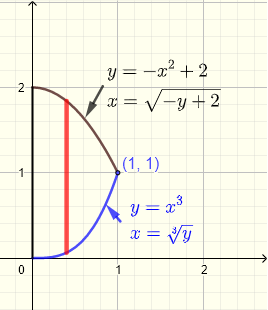
问题：计算二重积分 \( \displaystyle V = \iint_R (x+y) \;dy \;dx \)，其中区域 \( R \) 是由 \(y\)-轴、方程 \( y = x^3 \) 和 \( y = - x^2 + 2 \) 所围成的区域。

示例 2 的解答
我们首先分析区域 \( R \)，如下面的图所示。两条曲线的交点的 \( x \) 坐标由以下方程组的解给出：
\( y = x^3 \)
\(y = - x^2 + 2 \)
解上述方程组的一种方法是减去这两个方程并简化以消除 \( y \)，得到关于 \(x \) 的方程：
\( 0 = x^3 + x^2 - 2 \)
借助图形，很容易看出 \( x = 1 \) 是上述方程组的解，您可以通过分析进行检查。
通过将已找到的解 \( 1 \) 代入其中一个曲线的方程，可以找到交点的 \(y\) 坐标：\( y = (1)^3 = 1 \)。因此，交点是 \( (1,1) \)。
示例 2 的积分区域
1) 使用垂直条带
在给定垂直条带中，从 \( y = x^3 \) 到 \( y = - x^2 + 2 \) 的区域。对于整个区域，\( x \) 取值范围为 \( x = 0 \) 到 \( x = 1 \)。因此，积分区域 \( R \) 表示为： \( R \) ：\( 0 \le x \le 1 \) , \( x^3 \le y \le - x^2 + 2 \) 因此，积分可以如下计算：
\( \displaystyle V = \int_0^1 \int_{x^3}^{-x^2+2} (x+y) \;dy \;dx = \dfrac{803}{420}\)
示例 2 使用垂直条带描述的积分区域

2) 使用水平条带
在给定的水平条带中，从 \(y\)-轴 \( x = 0 \) 开始，到曲线 \( x = \sqrt[3]y \) 或曲线 \( x = \sqrt{- y+ 2} \) 结束。由于这两条不同的曲线，区域 \( R \) 可分为两个区域 \( R_1 \) 和 \( R_2 \)。
对于区域 \( R_1 \)，\( y \) 取值范围为 \( y = 0 \) 到 \( y = 1 \)；对于区域 \( R_2 \)，\( y \) 取值范围为 \( y = 1 \) 到 \( y = 2 \)。
因此，积分区域 \( R \) 分为两部分：
\( R_1 \) ：\( 0 \le x \le \sqrt[3]y \) , \( 0 \le y \le 1 \)
以及
\( R_2 \) ：\( 0 \le x \le \sqrt{- y+ 2} \) , \( 1 \le y \le 2 \)
因此，积分可以如下计算：
\( \displaystyle V = \iint_{R_1} (x+y) \;dx \;dy + \iint_{R_2} (x+y) \;dx \;dy \)

\( \displaystyle = \int_0^1 \int_{0}^{\sqrt[3]y} (x+y) \;dx \;dy + \int_1^2 \int_{0}^{\sqrt{-y+2}} (x+y) \;dx \;dy = \dfrac{803}{420}\)
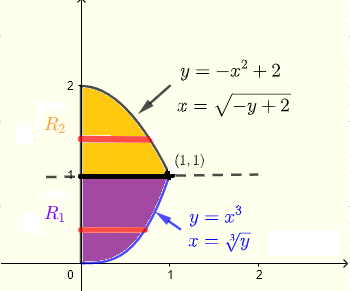
示例 2 使用水平条带描述的积分区域

当积分顺序取决于给定问题时的示例

在示例 3、4 和 5 中，我们展示了有时在二重积分中我们并没有两个积分顺序的选择。
示例 3、4 和 5 的目标是使用图形和示意图确定导致二重积分的解析计算的积分顺序。

示例 3
问题：求二重积分 \( \displaystyle V = \int _0^1 \int _y^1 (y + e^{-x^2}) dx dy \)（如可能）。如有必要，颠倒积分顺序以求解给定的积分。
示例 3 的解答
让我们从内积分开始
设 \( \displaystyle I = \int _y^1 (y+e^{-x^2}) dx \)
在尝试求解上面的 \( I \) 时，发现积分 \( \displaystyle I = \int _y^1 (e^{-x^2}) dx \) 无法解析完成。
根据给定的积分限，积分 \( V \) 的积分区域 \( R \) 可以表示为：
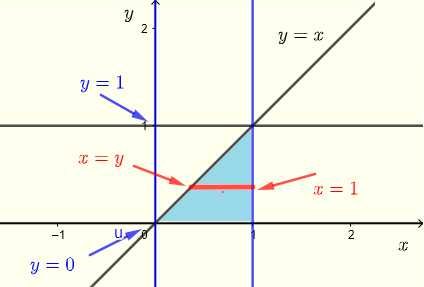
\( R \) ：\( y \le x \le 1 \) , \( 0 \le y \le 1 \)
如图所示为一组水平条带。

示例 3 使用水平条带描述的积分区域
现在让我们使用垂直条带来描述区域 \( R \)，如下面的图所示。
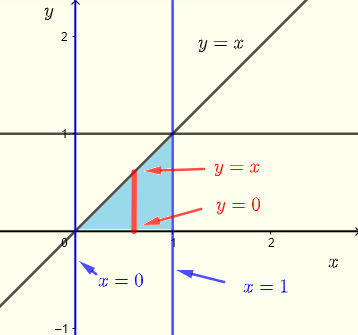
示例 3 使用垂直条带描述的积分区域
绘制积分区域 \( R \) 以查看是否可以通过改变积分顺序继续进行。
\( R \) ：\( 0 \le x \le 1 \) , \( 0 \le y \le x \)
积分 \( V \) 可以写为：
\( \displaystyle V = \int _0^1 \int _0^x (y + e^{-x^2}) dy dx \)
使用给定的内积分 \( I \) 计算
\( \displaystyle I = \int _0^x (y + e^{-x^2}) dy \)
\( = \left[ \dfrac{y^2}{2} + y e^{-x^2} \right]_0^x \)
\( = \dfrac{x^2}{2} + x e^{-x^2} \)
我们现在将 \( I \) 代入 \( V \) 并计算给定的积分
\( \displaystyle V = \int _0^1 (\dfrac{x^2}{2} + x e^{-x^2} ) dx \)
\( = \left[ \frac{x^3}{6}-\frac{1}{2}e^{-x^2} \right]_0^1 \)
\( = \dfrac{2}{3} - \dfrac{1}{2}e^{-1} \)

示例 4
求二重积分 \( \displaystyle V = \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dy \:dx \)，区域 \( R \) 如下图所示的蓝色阴影区域。
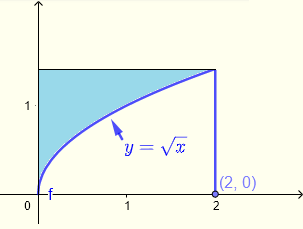
示例 4 的积分区域
示例 4 的解答
设内积分为 \( \displaystyle I = \int \left(\sqrt{1+y^3}+\:x\right) \; dy \)
很明显，这个积分难以解析完成。
我们交换积分顺序。
\( V = \displaystyle \iint_R \left(\sqrt{1+y^3}+\:x\right)\:dx \:dy \)
积分区域 \( R \) 可表示为：
\( R\) ：\( 0 \le x \le y^2 \) , \( 0 \le y \le \sqrt 2 \)
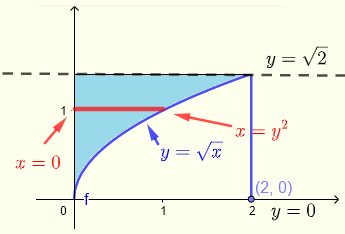
示例 4 使用水平条带描述的积分区域

\( \displaystyle V = \int _0^{\sqrt 2} \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx dy \)
计算内积分 \( I \)。
\( I = \displaystyle \int _0^{y^2} \left(\sqrt{1+y^3}+\:x\right) dx \)
\( = \left [ x \sqrt{1+y^3} + \dfrac{x^2}{2} \right]_0^{y^2} \)
简化结果
\( = y^2\sqrt{y^3+1}+\frac{y^4}{2} \)
将 \( I \) 代入 \( V \) 并计算外积分
\( \displaystyle V = \int _{0\:}^{\sqrt 2} \left(y^2\sqrt{y^3+1}+\frac{y^4}{2} \right) \; dy \)
计算上述积分
\( \displaystyle V = \left [ \frac{2}{9}\left(y^3+1\right)^{\frac{3}{2}}+\frac{y^5}{10} \right]_0^{\sqrt 2} \)
简化结果
\( V = \frac{2}{9}\left(\left(\sqrt{2}\right)^3+1\right)^{\frac{3}{2}}+\frac{\left(\sqrt{2}\right)^5}{10}-\dfrac{2}{9} \approx 2.00 \)

示例 5
求二重积分 \( \displaystyle V = \iint_R (x+y)\:dydx \) ，区域 \( R \) 由方程 \( x = (y-2)^2-2 \) 和 \( y = - x + 6 \) 所围成。
示例 5 的解答
如果使用垂直条带，由于在区间 \( -2 \le x \le 2 \) 和 \( 2 \le x \le 7 \) 中，\( y \) 的积分限不同，因此积分区域将有两部分，并且积分计算非常复杂。
因此我们使用水平条带。
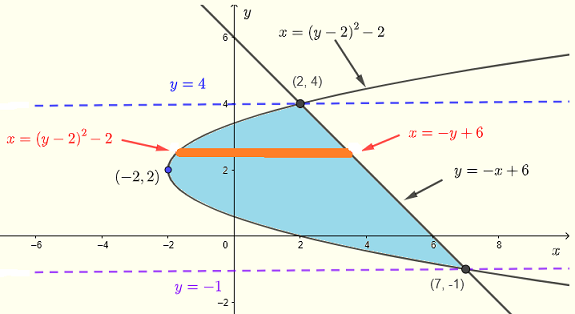
示例 5 使用水平条带描述的积分区域

积分区域 \( R \) 可表示为：
\( R\) ：\( (y-2)^2 - 2 \le x \le -y+6 \) , \( -1 \le y \le 4 \)
\( \displaystyle V = \int _{-1}^{4} \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \: dy \)
设内积分为 \( \displaystyle I = \int _{(y-2)^2 - 2}^{-y+6} (x+y)\:dx \)
计算该积分
\( I = \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \)
将 \( I \) 代入 \( V \) 并计算外积分
\( \displaystyle V = \int _{-1}^4 \left( \dfrac{-y^4+6y^3-13y^2+12y+32}{2} \right) \; dy \)
计算上述积分
\( \displaystyle V = \dfrac{1}{2} \left[-\dfrac{y^5}{5}+\dfrac{3y^4}{2}-\dfrac{13y^3}{3}+6y^2+32y\right]_{-1}^4 \)
求值
\( V = \dfrac{875}{12} \)
注意
作为练习，展示使用垂直条带时，二重积分表示为：
\( \displaystyle \int _{-2}^2\:\int _{2-\sqrt{x+2}}^{2+\sqrt{x+2}}\:\left(x+y\right)dydx+\int _2^7\:\int _{2-\sqrt{x+2}}^{-x+6}\:\left(x+y\right)dydx \)

上述问题的答案

第一部分：

积分区域

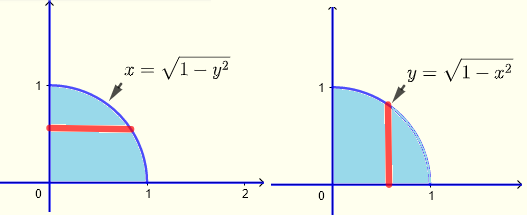
垂直条带
\( 0 \le x \le 1 \) , \( 0 \le y \le \sqrt{1-x^2} \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-x^2}}\:xy\:dy\:dx = 1/8 \)
水平条带
\( 0 \le x \le \sqrt{1-y^2} \) , \( 0 \le y \le 1 \)
\( \displaystyle \int _0^1\:\int _0^{\sqrt{1-y^2}}\:xy\:dx\:dy = 1/8\)
积分区域

垂直条带
\( 0 \le x \le 3\) , \( 0 \le y \le x \)
\( \displaystyle \int _0^3\:\int _0^x \:\sin(x^2)\:dy\:dx = \dfrac{1}{2}\left(-\cos \left(9\right)+1\right) \)
水平条带
\( y \le x \le 3 \) , \( 0 \le y \le 3 \)
\( \displaystyle \int _y^3\:\int _0^3\:\sin(x^2)\:dx\:dy \) 非常难以解析求解。

第二部分
\( \displaystyle V = \int _0^1 \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dxdy \)
计算内积分 \( I \)：
\( \displaystyle I = \int _{ \arcsin y}^{\frac{\pi }{2}}\:\left(xy\right)dx \)
\( = y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right) \)
现在将 \( I \) 代入积分 \( V \) 中：
\( \displaystyle V = \int _0^1 (y \left(\dfrac{\pi^2}{8} - \dfrac{\arcsin^2(y)}{2} \right)) dy \)
这在解析上很难完成。
让我们重新开始并交换积分顺序：
首先绘制积分区域 \( R \)
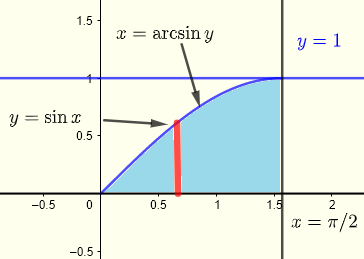
练习 3 的积分区域

\( \displaystyle V = \int _0^{\frac{\pi }{2}} \int _0^{\sin x} x \; y \; dy \;dx \)
设内积分 \( I = \int _0^{\sin x} x \; y \; dy \)
计算 \( I \)
\( I = x\frac{\sin ^2\left(x\right)}{2} \)
\( \sin^2(x) = \dfrac{1-\cos(2x)}{2} \)
\( I = \dfrac{x}{4}(1-cos(2x) \)
将 \( I \) 代入 \( V \)
\( \displaystyle V = \int _0^{\frac{\pi }{2}} (\dfrac {x}{4} - \dfrac {x}{4} \cos (2x) ) dx \)
分开积分
\( \displaystyle = \int _0^{\frac{\pi }{2}} \dfrac {x}{4} dx - \int _0^{\frac{\pi }{2}} \dfrac {x}{4} \cos (2x) dx \)
右边的积分使用分部积分法计算，得到
\( = \left[ \frac{x^2}{8} \right]_0^{\pi/2}- \left[\frac{1}{8} x \sin (2x)+\frac{1}{16}\cos (2x) \right]_0^{\pi/2} \)
求值
\( = \dfrac{\pi^2+4}{32} \)

一般区域上的二重积分