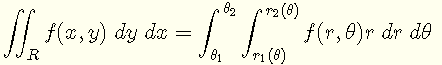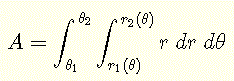目录
极坐标中的二重积分
本文展示了如何在极坐标下计算二重积分,以及在一般区域的积分示例,并附有详细的解决方案。这些示例还表明,将二重积分从直角坐标转换为极坐标可以使其更易于使用基本函数进行求解。
将二重积分转换为极坐标
将二重积分从直角坐标转换为极坐标的公式为[1]:
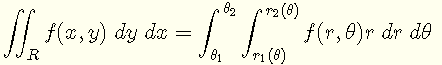
其中,直角坐标x和y与极坐标r和θ的关系为[6]:
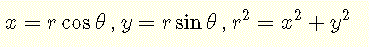
闭合区域R在极坐标中的面积A由下式给出:
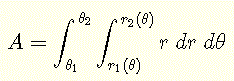
带详细解答的示例
示例 1
\( \) \( \) \( \) \( \)
问题:计算二重积分 \( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx \),其中区域 \( R \) 是平面上的圆 \( xy\)-平面,圆心在原点,半径等于 \( 1\)。
示例 1 的解答
给定的积分在直角坐标下无法用基本函数求解。让我们尝试将其转换为极坐标。
设 \( f(x,y) = \sqrt {1 - x^2 - y^2} \) 并将其表示为极坐标形式。
-example-1.gif)
\( r^2 = x^2 + y^2 \)
因此,函数 \( f(x,y) \) 的极坐标形式为
\( f(r,\theta) = \sqrt {1 - r^2} \)
积分区域 \( R \) 是一个圆,可以通过以下不等式定义:
\( R: \) \( 0 \le \theta \le 2\pi \) 且 \( 0 \le r \le 1 \)
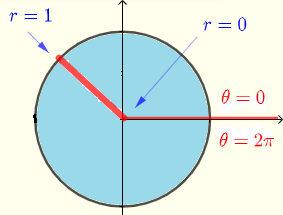
给定的直角坐标积分可以如下转换为极坐标积分:
\( \displaystyle V = \iint_R \sqrt {1 - x^2 - y^2} \;dy \;dx = \int_0^{2\pi} \int_0^{1} \sqrt{1-r^2} \; r \; dr \; d\theta \)
设 \( I \) 为定义的内积分:
\( \displaystyle I = \int_0^{1} \sqrt{1-r^2} \; r \; dr \)
\( = \left[ -\frac{1}{3}\left(1-r^2\right)^{\frac{3}{2}} \right]_0^1 = \dfrac{1}{3} \)
代入 \( I \) 并计算 \( V \):
\( \displaystyle V = \int_0^{2\pi} (1/3) \; d\theta \)
\( = \dfrac{1}{3} \left[ \theta \right]_0^{2\pi} \)
\( = \dfrac{2\pi}{3} \)
示例 2
问题:计算二重积分 \( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx \)
示例 2 的解答
给定的积分在直角坐标下不易计算,因此需要使用极坐标来简化计算。
让我们将 \( f(x,y) = e^{x^2+y^2} \) 表示为极坐标形式。
\( r^2 = x^2 + y^2 \)
因此,函数 \( f(x,y) \) 的极坐标形式为
\( f(r,\theta) = e^{r^2} \)
在直角坐标下,积分区域 \( R \) 由给定的积分限定义。
\( R: \) \( 0 \le x \le 1 \) 和 \( 0 \le y \le \sqrt{1-x^2} \)
我们通过图形解法求解不等式 \( y \le \sqrt{1-x^2} \)
将两边平方
\( y^2 \le 1-x^2 \)
将 \( x \) 和 \( y \) 的项移到左侧
\( y^2 + x^2 \le 1 \)
以上不等式表示原点 \( (0,0) \) 为圆心、半径为 \( 1 \) 的圆内或圆上的所有点 \( (x,y) \)。
将所有不等式组合在一起,积分区域 \( R \) 如下图所示。

上述区域在极坐标下如图所示

其定义如下:
\( R: \) \( 0 \le \theta \le \pi/2 \) 且 \( 0 \le r \le 1 \)
现在可以将积分转换为极坐标形式
\( \displaystyle V = \int_0^{1} \int_0^{\sqrt{1-x^2}} e^{x^2+y^2} \; dy \; dx = \int_0^{\pi/2} \int_0^1 e^{r^2} r \; dr \; d\theta \)
设 \( I \) 为定义的内积分:
\( \displaystyle I = \int_0^1 e^{r^2} r \; dr \)
\( = \left[ \dfrac{1}{2} e{r^2} \right]_0^1 \)
\( = \dfrac{1}{2} (e - 1) \)
代入 \( I \) 并计算 \( V \)
\( \displaystyle V = \int_0^{\pi/2} \dfrac{1}{2} (e - 1) \; d\theta \)
\( = \dfrac{\pi}{4} (e - 1) \)
示例 3
问题:将积分 \( \displaystyle V = \iint_R {x^2+y^2} \; dy \; dx \) 转换为直角坐标和极坐标形式,且 \( R \) 是 \( xy \) 平面上圆心为 \( (1,0) \) 且半径为 \( 1 \) 的圆,并计算该积分。
示例 3 的解答
我们首先绘制积分区域 \( R \) 并定义其直角坐标和极坐标形式。
1) 直角坐标
圆心为 \( (1,0) \) 且半径为 \( 1 \) 的圆的方程为
\( (x-1)^2 + y^2 = 1 \)
展开并将同类项合并
\( x^2 - 2x + y^2 = 0 \)
求解该方程得到两个解
\( y = \pm \sqrt {2x-x^2} \)
使用垂直条带,区域 \( R \) 可以通过以下不等式定义:
\( R: \) \( 0 \le x \le 2 \) 和 \( - \sqrt {2x-x^2} \le y \le \sqrt {2x-x^2} \)
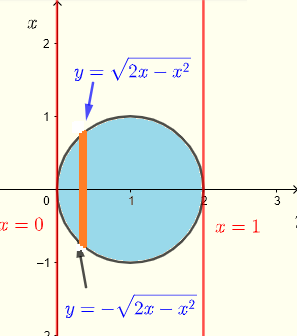
积分可以表示为
\( \displaystyle V = \int_0^2 \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \; dx \)
设 \( I_1 \) 为定义的内积分:
\( \displaystyle I_1 = \int_{-\sqrt {2x-x^2}}^{\sqrt {2x-x^2}} \; \; (x^2+y^2) \; dy \)
计算 \( I_1 \):
\( \displaystyle I_1 = 2x^2\sqrt{2x-x^2}+2\cdot \frac{\left(2x-x^2\right)^{\frac{3}{2}}}{3} \)
在直角坐标下计算外部积分的下一步非常具有挑战性。
2) 极坐标
使用从原点到圆上某点的条带:在原点处 \( r = 0 \);在圆上 \( r = \sqrt {x^2 + y^2} \)
我们将圆的方程 \( x^2 + y^2 = 2x \) 转换为极坐标形式。
根据直角坐标和极坐标之间的关系[6],我们有
\( r^2 = x^2 + y^2 \) 和 \( x = r \cos \theta \)
在方程 \( x^2 + y^2 = 2x \) 中用 \( r^2 \) 替换 \( x^2 + y^2 \) 并用 \( r \cos \theta \) 替换 \( x \),得到
\( r^2 = 2 r \cos \theta \)
将上述方程的两边除以 \( r \)
\( r = 2 \cos \theta \)
在极坐标下,区域 \( R \) 可以通过以下不等式定义:
\( R: \) \( -\pi/2 \le \theta \le \pi/2 \) 且 \( 0 \le r \le 2 \cos \theta \)

使用 \( r^2 = x^2 + y^2 \)
将积分写为极坐标形式:
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} \int_{0}^{2 \cos \theta} r^2 \; r \; dr \; d\theta \)
设内积分 \(I \) 为:
\( \displaystyle I = \int_{0}^{2 \cos \theta} r^2 \; r \; dr \)
计算:
\( \displaystyle I = \left[ r^4 / 4 \right]_{0}^{2 \cos \theta} \)
\( \displaystyle I = 4 cos^4 \theta \) (方程 1)
将上述表达式中的幂次 \( \cos^4 \theta \) 降低
\( \cos^4 \theta = \cos^2 \theta \cos^2 \theta \)
使用降幂恒等式
\( \cos^2 \theta = \dfrac{cos (2\theta) + 1}{2} \)
因此
\( \cos^4 \theta = \left( \dfrac{\cos (2\theta) + 1}{2} \right)^2 \)
\( = \dfrac{\cos^2(2\theta) + 2 \cos (2\theta) + 1}{4} \)
再使用一次降幂恒等式
\( \cos^4 \theta = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{8} + 3/8 \)
我们现在将上述表达式代入方程 1 中,得到
\( I = \dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 \)
将 \( I \) 代入积分并计算
\( \displaystyle V = \int_{-\pi/2}^{\pi/2} (\dfrac{\cos(4\theta) + 4\cos(2\theta) }{2} + 3/2 ) \; d\theta \)
\( \displaystyle = \left[ \frac{1}{2}\left(\frac{1}{4}\sin \left(4\theta\right)+2\sin \left(2\theta\right)\right)+\frac{3}{2}\theta \right]_{-\pi/2}^{\pi/2} \)
\( = \dfrac{3\pi}{2} \)
给定的积分使用极坐标计算要容易得多。
示例 4
问题:将积分 \( \displaystyle V = \int_{-1}^0 \int_{-\sqrt{1-x^2}}^0 \dfrac{\sqrt{x^2+y^2}}{1+\sqrt{x^2+y^2}} \; dy \; dx \) 转换为极坐标形式并计算。
示例 4 的解答
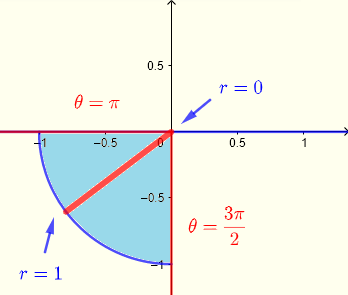
从直角坐标中的积分限可以推断出积分区域 \( R \),它是第三象限的四分之一圆,如图所示
\( R: \) \( 0 \le x \le 2 \) 和 \( - \sqrt {1-x^2} \le y \le 0 \)
其图形如下所示
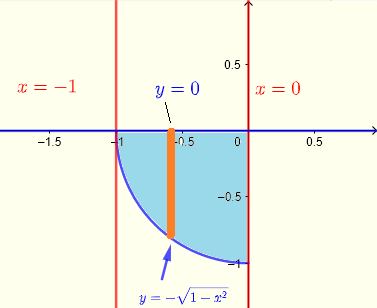
在极坐标中使用从原点到四分之一圆上某点的条带:在原点处 \( r = 0 \);在圆上 \( r = 1 \),积分区域 \( R \) 在极坐标下可以定义为:
\( R: \) \( \pi \le \theta \le 3\pi/2 \) 和 \( 0 \le r \le 1 \)
使用 \( r = \sqrt { x^2 + y^2 } \)
将给定的积分写为极坐标形式:
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r}{1+r} \; r \; dr \; d\theta \)
\( \displaystyle = \int_{\pi}^{3\pi/2} \int_{0}^{1} \dfrac{r^2}{1+r} \; dr \; d\theta \)
使用除法将被积函数 \( \dfrac{r^2}{1+r} \) 展开如下
\( \dfrac{r^2}{1+r} = r-1+\frac{1}{r+1} \)
将被积函数的展开形式代入积分中
\( \displaystyle V = \int_{\pi}^{3\pi/2} \int_{0}^{1} (r-1+\frac{1}{r+1}) \; dr \; d\theta \)
积分:
\( \displaystyle = \int_{\pi}^{3\pi/2} \left[ \dfrac{r^2}{2} - r + ln |r+1| \right]_0^1 d\theta \)
计算:
\( \displaystyle = \int_{\pi}^{3\pi/2} (\ln (2)-\dfrac{1}{2}) d\theta \)
积分:
\( = \left( \ln (2)-\dfrac{1}{2} \right) \left[ \; \theta \; \right]_{\pi}^{3\pi/2} \)
计算:
\( V = \dfrac{\pi}{2} \left( \ln (2)-\dfrac{1}{2} \right) \)
更多带答案的问题
第一部分
将每个积分转换为极坐标并求解。
-
\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
-
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
第二部分
-
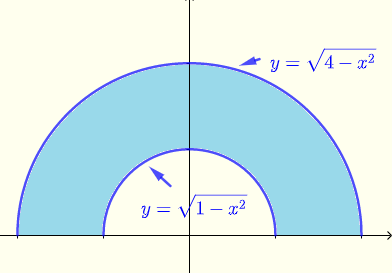
求解 \( \displaystyle V = \iint_R \: e^{\sqrt{x^2+y^2}} \; dx \; dy \),其中 \( R \) 是下图中蓝色区域。
以上问题的答案
第一部分:
-
直角坐标(左侧)和极坐标(右侧)中积分区域的图形如下所示。

\( \displaystyle V = \int_{-1}^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \; \; \sin(x^2+y^2) \;dy \;dx \)
将上述积分转换为极坐标形式:
\( \displaystyle V = \int_{0}^{2\pi} \int_0^1 \; \; \sin(r^2) \;r \; dr \;d\theta \)
求解:
\( = \pi (1 -\cos 1) \)
-
直角坐标(左侧)和极坐标(右侧)中积分区域的图形如下所示。
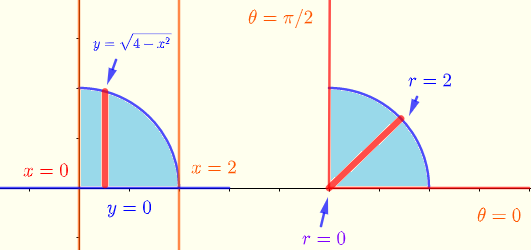
\( \displaystyle V = \int _0^2\:\:\int _0^{\sqrt{4-x^2}} \sqrt{x^2+y^2} \:\;dy\:\;dx\: \)
将上述积分转换为极坐标形式:
\( \displaystyle V = \int_{0}^{\pi/2} \int_0^2 \; \; r^2 \; dr \;d\theta \)
求解:
\( = \dfrac{4\pi }{3} \)
第二部分
使用直角坐标求解给定的积分
\( \displaystyle V = \int_{-2}^{2} \int_0^{\sqrt{4-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx - \int_{-1}^{1} \int_0^{\sqrt{1-x^2}} \: e^{\sqrt{x^2+y^2}} \; dy \; dx \)
使用基本函数进行计算相当具有挑战性。
极坐标中的积分区域如下图所示
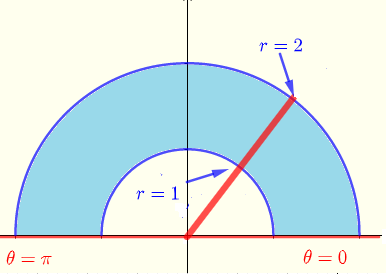
\( R: \) \( 0 \le \theta \le \pi \) 和 \( 1 \le r \le 2 \)
给定:
\( \displaystyle V = \iint_R \: e^{\sqrt{x^2+y^2}} \; dx \; dy \)
给定的积分在极坐标下为
\( \displaystyle V = \int_0^{\pi} \; \int_1^2 \: r e^{r} \; dr \; d\theta \)
求解:
\( = \pi e^2 \)
更多参考和链接
- Joel Hass, 加利福尼亚大学戴维斯分校;Maurice D. Weir,海军研究生院;George B. Thomas, Jr.,麻省理工学院;《大学微积分:早期超越法》,第三版,波士顿哥伦布,2016年,Pearson出版。
- 二重积分计算
一般区域的二重积分
- Howard Anton, Irl C. Bivens, Stephen Davis;《微积分:早期超越法》;Willey出版社,2012年。
- Gilbert Strang;麻省理工学院,《微积分》,Wellesley-Cambridge出版社,1991年。
- 极坐标
- 极坐标与直角坐标的相互转换
工程数学示例与解答
-example-1.gif)