目录
二重积分的应用 二重积分 计算体积和面积的例子,并提供了详细的解决方案。
\( \)\( \)\( \)
使用二重积分计算体积
给定表面 \( z = f(x,y) \) 在区域 \( R \) 之上且在 \( xy\)-平面之下,且 \( f(x,y) \ge 0 \),则固体的体积 \( V \) 由以下二重积分给出 [6] :
\[ \displaystyle V = \iint_R f(x,y) \;dy \;dx \]
例子 1
例子 1 的解决方案
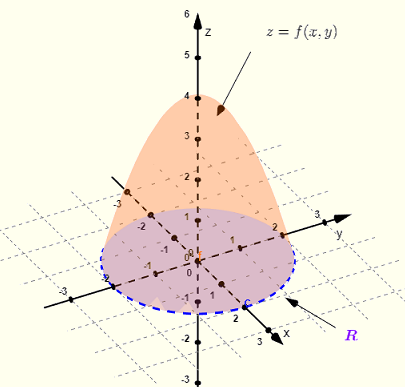
图1 - 位于平面 \( z = 0 \) 和抛物面 \( z = 4 - x^2 - y^2 \) 之间的体积
积分区域 \( R \) 是抛物面和平面 \( z =0 \) 的交点,通过在抛物面方程中设置 \( z = 0 \) 得到:
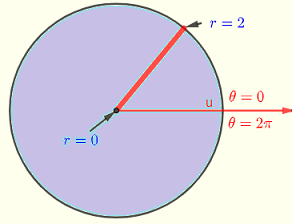
图2 - 积分区域 \( R \) 是一个圆,圆心为 \( (0,0) \) ,半径为 \( 2 \)
由于积分区域是一个圆,所以使用极坐标中的二重积分 更为有效。
例子 2
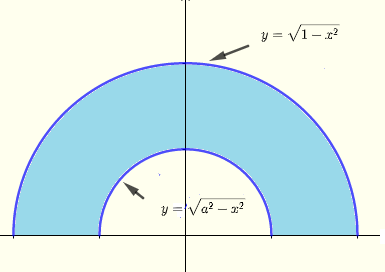
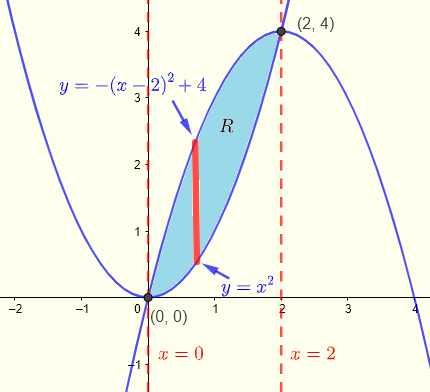
图3 - 给定的积分区域
例子 2 的解决方案
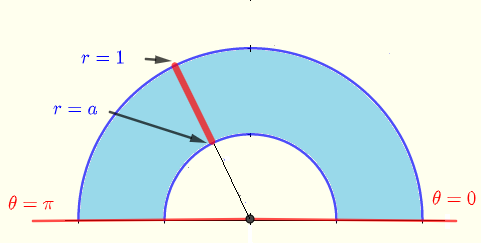
图4 - 极坐标中的积分区域
极坐标中的积分区域可以定义为:
例子 3
例子 3 的解决方案
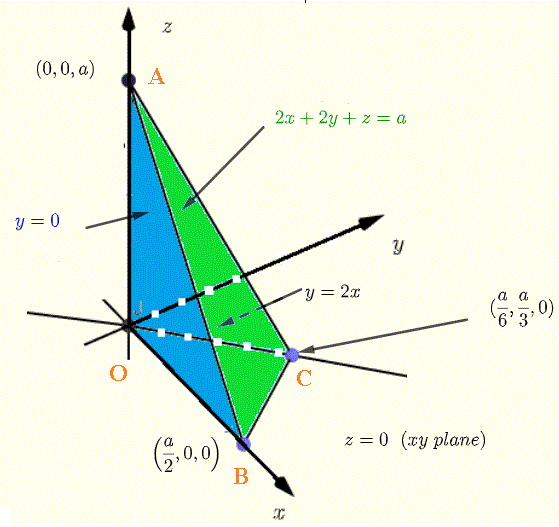
图5 - 定义固体的平面
首先找到由三个顶点 \( O , B \) 和 \( C \) 定义的三角形的积分区域。
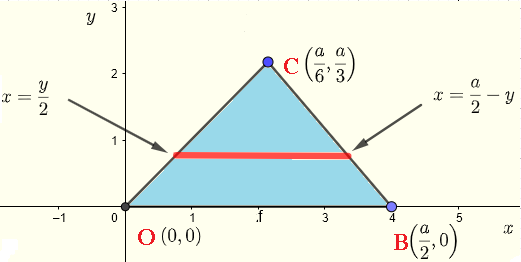
图6 - 积分区域
注意: 您可以检查上面的结果是否与使用四面体体积的非常著名公式获得的结果一致:
使用二重积分计算面积
平面 \( xy\) 上区域 \( R \) 的面积 \( A \) 由以下二重积分给出 [6] :
\[ A = \displaystyle \iint_R 1 \;dy \;dx \]
例子 4
例子 4 的解决方案
图7 - 积分区域
两条曲线相交于它们的方程组成的方程组的解处:
例子 5
例子 5 的解决方案
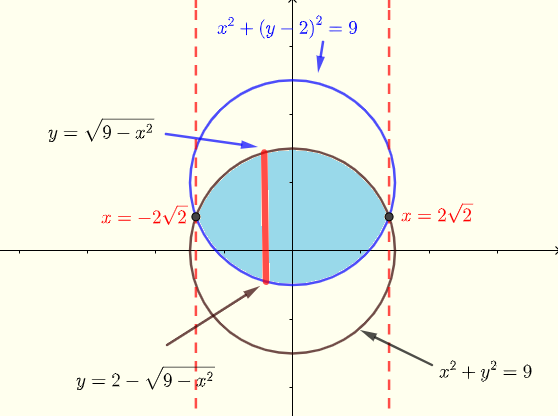
图7 - 两个圆的公共区域
交点通过解以下方程组求得:
注意: 积分 \( \int \sqrt{9-x^2}dx \) 的详细内容包含在附录A 中。
附录
附录A
更多问题与答案
第一部分
求出由平面 \( x = 1 \) 、 \( x =2 \) 、 \( y = 0 \) 、 \( y = 2 \) 、 \( z = 0 \) 所包围,并位于双曲抛物面 \( z = 20 + x^2 - 2y^2 \) 下的固体的体积。
求出由平面 \( y = 2 \) 、 \( z = 0 \) 所包围,并位于表面 \( z = 9-x^2 \) 下的固体的体积。
求出由圆柱 \( 9 - x^2 - y^2 = 0 \) 、 \( z = 0 \) 所包围,并位于平面 \( z=5+0.5x+y \) 下的固体的体积。
求出 \( xy \) 平面上由圆 \( x^2 + y^2 = 4 \) 和直线 \( y = - 1 \) 围成的区域的面积。
上述问题的答案
第一部分:
\( \dfrac{118}{3} \)
\( 72 \)
\( 45 \pi \)
\( \dfrac{8\pi }{3}+\sqrt{3} \)
更多参考文献与链接
二重积分计算
一般区域上的二重积分
极坐标中的二重积分
Howard Anton, Irl C. Bivens, Stephen Davis ; Calculus: Early Transcendentals; Wiley, 2012.
Gilbert Strang; MIT, Calculus, Wellesley-Cambridge Press, 1991
Joel Hass, University of California, Davis; Maurice D. Weir Naval Postgraduate School; George B. Thomas, Jr. Massachusetts Institute of Technology; University Calculus, Early Transcendentals, Third Edition, Boston Columbus, 2016, Pearson.
工程数学与示例及解决方案