一个交互式在线图形计算器，用于可视化脉冲 \( f(t) \) 及其傅里叶变换 \( F(\omega) \)。\( t \) 表示时间，\( \omega \) 表示角频率。
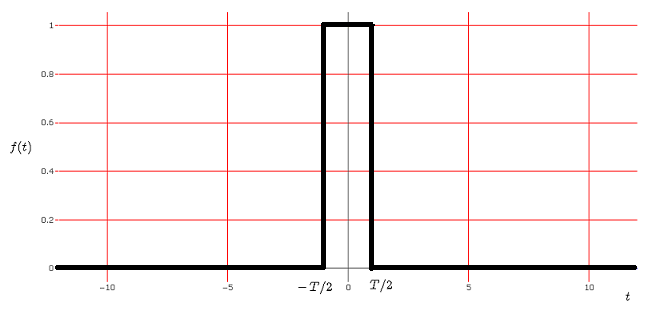\( f(t) \) 的傅里叶变换定义为
\[ F(\omega) = \int_{-\infty}^{+\infty} f(t) e^\left( - j \omega t\right) dt \\
= \int_{-T/2}^{+T/2} 1 \cdot e^\left( - j \omega t\right) dt \\
= \left[ \dfrac{ e^\left( - j \omega t \right)}{-j \omega} \right]^{T/2}_{-T/2}
\]
求解并简化为
\[ F(\omega) = \dfrac{\sin(\omega(T/2))}{\omega/2}
\]
T =