用解决方案解决交流电路问题

目录

基尔霍夫定律和欧姆定律被扩展并用于利用复数形式的阻抗来解决交流电路问题。
所有的量如电压、电流和阻抗都用复数的标准形式和极坐标形式表示。

复数的回顾

虚数单位定义为 \( j = \sqrt {-1} \) 或 \( j^2 = - 1 \)
复数 \( Z \) 在标准形式 \( Z = a + j b \) 中可以写成极坐标形式为
\( Z = r \; \angle \; \theta \)
其中 \( r \) 和 \( \theta \) 分别是 \( Z \) 的模和辐角，定义为
\( r = |Z| = \sqrt {a^2 + b^2} \) 和 \( \theta = \arctan \left( \dfrac{b}{a} \right) \)，范围在 \( -\pi \lt \theta \le \pi \)
在极坐标形式下更容易对复数进行除法或乘法运算
设 \( Z_1 = r_1 \; \angle \; \theta_1 \) 和 \( Z_2 = r_2 \; \angle \; \theta_2 \)
\( Z_1 \cdot Z_2 = r_1 \cdot r_2 \; \angle \; \theta_1 + \theta_2 \)
\( \dfrac{Z_1}{Z_2} = \dfrac{r_1}{r_2} \; \angle \; \theta_1 - \theta_2 \)

带解决方案的问题

问题 1
在下图所示电路中，已知电压源 \( v_i = 10 \cos (\omega t ) \) V，电阻 \( R = 100 \; \Omega \)，电容 \( C = 0.47 \; \mu F \)，频率 \( f = 1 \) kHz 和 \( \omega = 2 \pi f \)，求电阻 \( R \) 和电容 \( C \) 上的电流和电压的模和相移（极坐标形式）。

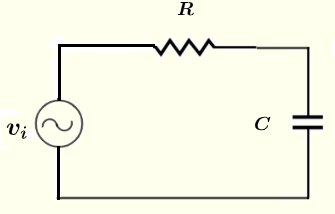
问题 1 解决方案
设 \( V_i \)、\( V_R \)、\( V_C \) 和 \( I \) 分别是 \( v_i \)、\( v_R \)、\( v_C \) 和 \( i \) 的复数形式。


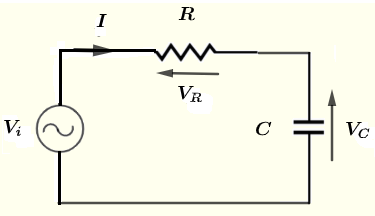
使用基尔霍夫的电压定律来写出方程
\( V_i - V_R - V_C = 0\)      (1)
电阻 \( R \) 和电容 \( C \) 的复数阻抗为
\( Z_R = R \; \)       (实数)
\( Z_C = - j \dfrac{1}{\omega C} \; \)       (虚数)

使用欧姆定律来写
\( V_R = Z_R I \) 和 \( V_C = Z_C I \)
将 \( V_R \) 和 \( V_C \) 的表达式代入方程 (1)
\( V_i - Z_R I - Z_C I = 0 \)
求解 \( I \)
\( I = \dfrac{V_i}{Z_R + Z_C} \)

使用欧姆定律计算 \( V_R \) 和 \( V_C \) 如下：
\( V_R = Z_R I = \dfrac{V_i Z_R }{Z_R + Z_C} \)

\( V_C = Z_C I = \dfrac{V_i Z_C }{Z_R + Z_C} \)


复数极坐标形式的 \( v_i = 10 \cos (\omega t ) \) 可以写成：
\( V_i = 10 \; \angle \; 0 \)

现在将 \( V_i \)、\( Z_R \) 和 \( Z_C \) 代入它们的表达式得到
\( I = \dfrac{10 \; \angle \; 0}{R - j \dfrac{1}{\omega C}} \)

\( V_R = \dfrac{10 R \; \angle \; 0 \; }{R - j \dfrac{1}{\omega C}} \)

\( V_C = \dfrac{ (10 \; \angle \; 0 \;) (- j \dfrac{1}{\omega C}) }{R - j \dfrac{1}{\omega C}} \)

设所有上述表达式的分母为 \( Z_D = R - j \dfrac{1}{\omega C} \) 并将其改写为复数形式
\( Z_D \) 的模为：\( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} \)

\( Z_D \) 的辐角：\( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-1}{R \omega C} \)

现在将复数 \( - j \dfrac{1}{\omega C} \) 重写为极坐标形式
\( - j \dfrac{1}{\omega C} = \dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2} \)

现在将所有复数量代入 \( I \)、\( V_R \) 和 \( V_C \) 中的极坐标形式并重写
\( I = \dfrac{10 \; \angle \; 0}{ | Z_D | \; \angle \; \phi} \)

\( V_R = \dfrac{10 R \; \angle \; 0 \; }{ | Z_D | \; \angle \; \phi} \)

\( V_C = \dfrac{10 \; \angle \; 0 \; (\dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2}) }{ | Z_D | \; \angle \; \phi} \)

简化上述表达式：

\( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi \)

\( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi \)

\( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi \)

现在将所有已知量代入它们的数值
\( \omega = 2 \cdot \pi \cdot f = 2 \cdot \pi 10^3 = 2000 \pi \)
\( | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} = \sqrt {100^2 + \dfrac{1}{(2000 \pi)^2 (0.47 \cdot 10^{-6})^2}} = 353.08 \; \Omega \)
\( \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-\dfrac{1}{2000 \pi \cdot 0.47 \cdot 10^{-6} }}{100} = -73.55^{\circ} \)
因此

\( I = \dfrac{10} { | Z_D | } \; \angle \; - \phi = 0.0283 \; \angle \; 73.55^{\circ} \)
\( I \) 的模为 \( 0.02832 \; A\) ，相移为 \( 73.55^{\circ} \)

\( V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi = 2.832 \; \angle \; 73.55^{\circ} \)
\( V_R \) 的模为 \( 2.832 \; V\) ，相移为 \( 73.55^{\circ} \)

\( V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi = 9.591 \; \angle \; -16.45^{\circ} \)
\( V_C \) 的模为 \( 9.591 \; V\) ，相移为 \( -16.45^{\circ} \)

问题 2

在下图所示电路中，已知电压源 \( v_i = 10 \cos (\omega t ) \; V \)，电阻 \( R = 100 \; \Omega \)，电容 \( C = 0.47 \; \mu F \)，电感 \( L = 300 \; mH \)，频率 \( f = 2 \) kHz 和 \( \omega = 2 \pi f \)，求输出电压 \( v_o \) 的模和相移（极坐标形式）。


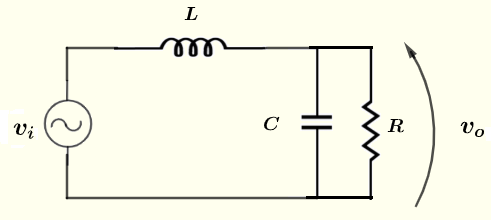
问题 2 解决方案
设 \( I \)、\( V_i \) 和 \( V_0 \) 分别是 \( i \)、\( v_i \) 和 \( v_o \) 的复数形式。
\( V_i \) 可以写成极坐标形式如下
\( V_i = 10 \; \angle \; 0 \)
电阻 \( R \) 的阻抗为
\( Z_R = R \; \)
电容 \( C \) 的阻抗为
\( Z_C = - j \dfrac{1}{\omega C} \; \)
电阻 \( R \) 和电容 \( C \) 并联。电阻 \( R \) 和电容 \( C \) 的等效阻抗 \( Z \) 为

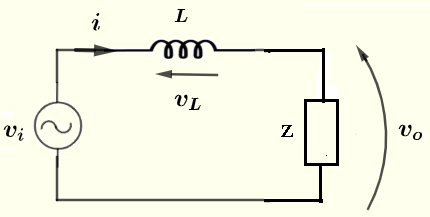
\( Z = \dfrac{Z_R \cdot Z_C}{Z_R + Z_C} \)
电感 \( L \) 的复数阻抗 \( Z_L \) 表示为
\( Z_L = j \omega L \)
使用基尔霍夫的电压定律来写出方程
\( V_i - V_L - V_0 = 0\)      (1)
使用欧姆定律来写
\( V_L = Z_L I \) 和 \( V_0 = Z I \)
将 \( V_L \) 和 \( V_0 \) 的表达式代入方程 (1)
\( V_i - Z_L I - Z I = 0 \)
求解 \( I \)
\( I = \dfrac{V_i}{ Z_L + Z} \)
使用欧姆定律来写
\( V_o = Z I = \dfrac{Z}{ Z_L + Z} V_i\)
代入已知量以找到数值
\( \omega = 2 \pi f = 2 \pi \cdot 2000 = 4000 \pi \)
\( Z_R = R = 100 \)
\( Z_C = - j \dfrac{1}{\omega C} = - j \dfrac{1}{4000 \pi \cdot 0.47 \cdot 10^{-6}} = - 169.314 j \)

\( Z = \dfrac{R \cdot Z_C}{R + Z_C} \) ( (\( R \) 和 \( C \) 并联)

\( = \dfrac{100 \cdot (- 169.314 j)}{100 - 169.314 j } = 74.138 -43.787 j\)
以及
\( Z_L = j \omega L = 4000 \pi \cdot 300 \cdot 10^{-3} j = 3769.911 j \)
\( V_o = \dfrac{Z}{ Z_L + Z} V_i \)

\( = \dfrac{Z}{ Z_L + Z} V_i \)

\( = \dfrac{74.138 -43.787 j}{ 3769.911 j + 74.138 -43.787 j} V_i \)
简化
\( = (-0.01135 -0.02012 j) V_i \)
将复数 \( (-0.01135 -0.02012 j) \) 写成极坐标形式并代入 \( V_i \) 的极坐标形式。
\( = ( 0.02310 \angle -119.43^{\circ} ) (10 \; \angle \; 0) \)
简化
\( V_o = 0.23 \; \angle \; -119.43^{\circ} \)

问题 3

在下图所示电路中，已知电压源 \( v_i = 10 \cos (\omega t ) \; V \)，电阻 \( R_1 = 220 \; \Omega \)、\( R_2 = 2.2 \; k\Omega \)、\( R_3 = 1 \; k\Omega \)，电容 \( C_1 = 0.47 \; \mu F \)、\( C_2 = 1.5 \; \mu F \)、电感 \( L = 30 \; mH \)，频率 \( f = 2.5 \) kHz 和 \( \omega = 2 \pi f \)，求输出电压 \( v_o \) 的模和相移（极坐标形式）。

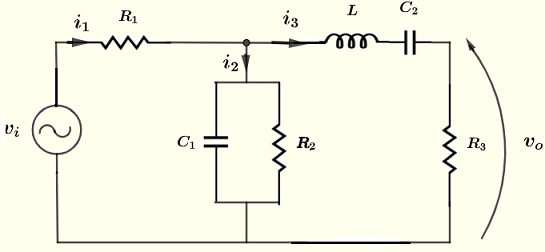
例子 3 解决方案
设 \( I_1 \)、\( I_2 \)、\( I_3 \)、\( V_i \) 和 \( V_0 \) 分别是 \( i_1 \)、\( i_2 \)、\( i_3 \)、\( v_i \) 和 \( v_o \) 的复数形式。
\( V_i \) 可以写成极坐标形式如下
\( V_i = 10 \; \angle \; 0 \)
\( V_o \) 可以通过欧姆定律计算
\( V_o = R_3 I_3\)
因此我们需要计算 \( I_3 \)
将阻抗分组，如下图所示：
\( Z_1 = R_1 \)
\( Z_2 = \dfrac{R_2 ( - \dfrac{1}{\omega C_1} j)}{R_2 - \dfrac{1}{\omega C_1} j} \)      ( \( C_1 \) 和 \( R_2 \) 并联)
\( z_3 = R_3 + j \omega L - \dfrac{1}{ \omega C_2} j \)      ( \( C_2 \)、\( L \) 和 \( R_3 \) 串联)

基尔霍夫的电压定律应用于两个闭环，得到两个方程
\( V_i - V_{z_1} - V_{z_2} = 0 \)
\( V_{z_2} - V_{z_3} = 0 \)
应用欧姆定律写出 \( V_{z_1} = Z_1 I_1 \)、\( V_{z_2} = Z_2 I_2 \) 和 \( V_{z_3} = Z_3 I_3 \) 并将其代入上述方程得到只包括电流的方程。
\( V_i - Z_1 I_1 - Z_2 I_2 = 0 \)     (1)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (2)
现在我们使用基尔霍夫电流定律在节点A写出
\( I_1 = I_2 + I_3 \)     (3)
我们有三个方程三个未知数 \( I_1 \)、\( I_2 \) 和 \( I_3 \)，但我们只需要 \(I_3\)。
使用方程 (3) 将方程 (1) 中的 \( I_1 \) 替换为 \( I_2 + I_3 \)，从而消除方程中的 \( I_1 \)，最终得到两个方程两个未知数的系统。
\( V_i - Z_1 ( I_2 + I_3) - Z_2 I_2 = 0 \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
将上述方程组改写为标准形式
\( (Z_1 + Z_2 ) I_2 + Z_1 I_3 = V_i \)     (4)
\( Z_2 I_2 - Z_3 I_3 = 0 \)     (5)
使用行列式求解上述方程组
\( I_3 = \dfrac{\begin{vmatrix} Z_1 + Z_2 & V_i \\ Z_2 & 0 \end{vmatrix}}{\begin{vmatrix} Z_1 + Z_2 & + Z_1 \\ Z_2 & -Z_3 \end{vmatrix}} \)
计算行列式以求解
\( I_3 = \dfrac{Z_2}{(Z_1+Z_2)Z_3 + Z_1 Z_2} V_i \)

数值计算
\( \omega = 2 \pi f = 5000 \pi \)
\( Z_1 = 220 \)
\( Z_2 = \dfrac{2200 ( - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j)}{2200 - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j} \)

\( Z_2 = 8.30804 -134.93950 j \)

\( z_3 = 1000 + 5000 \pi \cdot 30 \cdot 10^{-3} j - \dfrac{1}{ 5000 \pi \cdot 1.5 \cdot 10^{-6}} j \)
\( Z_3 = 1000 + 428.79757 j \)
\( I_3 = (0.00013 - 0.00043 j)V_i = 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0\)
\( V_0 = R_3 I_3 = 1000 \cdot 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0 \)
简化
\( V_0 = 4.4 \angle -73.18^{\circ} V \)

更多带答案的问题

问题 4
已知 \( v_i = 10 \angle 0^{\circ} \)，\( R = 200 \; \Omega \)，电容 \( C = 0.47 \; \mu F \)，电感 \( L = 40 \; mH \)，频率 \( f = 1 \) kHz。
求电流 \( I \) 通过电感器时的电流和电压 \( V_0 \) 的复数形式。

问题 4 答案

答案：\( I = 0.047 \angle -47.84^{\circ}\) ，\(V_0 = 11.38 \angle 42.16^{\circ} \)

问题 5
已知 \( v_i = 10 \angle 0^{\circ} \)，\( R_1 = 100 \; \Omega \)，电容 \( C = 0.47 \; \mu F \)，电阻 \( R_2 = 120 \; \Omega \)、\( R_3 = 200 \; \Omega \)、\( R_4 = 400 \; \Omega \)，电感 \( L = 20 \; mH \)，频率 \( f = 2 \) kHz。
求电流 \( I_1 \)、\( I_2 \)、\( I_3 \) 以及各电阻上的电压的复数形式。

问题 5 答案
答案：
电流：\( I_1 = 0.054 \angle 10.55^{\circ} \; ， \; I_2 = 0.048 \angle 23.01^{\circ} \; ， \; I_3 = 0.013 \angle -42.22^{\circ} \)
电压：\( V_{R_1} = 5.49 \angle 10.55^{\circ} \; ， \; V_{R_2} = 4.71 \angle -12.32^{\circ} \; ， \; V_{R_3} = 2.60 \angle -42.22^{\circ} \; ， \; V_{R_4} = 2.77 \angle 15.63^{\circ} \)

更多参考资料和链接