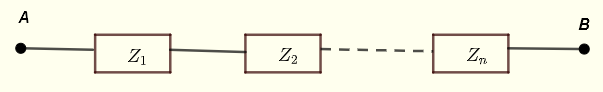
A和B点之间的等效阻抗为
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
本文讨论了如何使用复数阻抗来计算交流电路中串联和并联阻抗的等效阻抗。所有步骤均使用符号计算展示,然后使用数值计算。
由于在交流电路中符号 \( i \) 用于表示电流,这里使用 \( j \) 作为虚数单位,定义为 \( j^2 = -1 \) 或 \( j = \sqrt{-1} \)。
设 \( Z_1 \) , \( Z_2 \) ... \( Z_n \) 为串联阻抗,如下图所示。
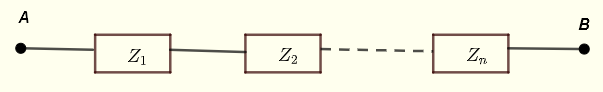
A和B点之间的等效阻抗为
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
示例 1
求下图所示串联RLC电路的复数阻抗,已知:
频率 \( f = 1 \; kHz \) , \( C = 10 \; \mu F \) , \( L = 10 \; mH \) 和 \( R = 100 \; \Omega \)

问题 1 的解决方案
设
\( Z_R = R \) , \( Z_C = \dfrac{1}{j \omega C} = \dfrac{-j}{\omega C} \) , \( Z_L = j \omega L\)
应用串联电路的阻抗规则
\( Z_{AB} = Z_R + Z_C + Z_L = R - \dfrac{j}{\omega C} + j \omega L \)
设
\( X_L = \omega L = 2 \pi f L \) 和 \( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} \)
将 \( Z_{AB} \) 重写如下
\( Z_{AB} = R + j(X_L - X_C) \)
代入数值
\( X_L = \omega L = 2 \pi f L = 2 \pi 10^3 10^{-2} = 62.83 \Omega \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} = \dfrac{1}{2 \pi 10^3 10^{-5} } = 15.92 \Omega \)
合并虚数项
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) \)
简化
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) = 100 + 46.91 j\)
将上述结果写成指数形式
\( Z_{AB} = \sqrt {100^2 + 46.91^2} e^{j \arctan{\dfrac{46.91}{100}}} = 110.45 e^{j 0.44} \)
\( Z_{AB} \) 写成相量形式
\( Z_{AB} = 110.45 \angle 0.44 \; 弧度 = 110.45 \angle 25.13^{\circ} \)
可以使用串联RLC电路阻抗计算器进行更多练习。
设 \( Z_1 \) , \( Z_2 \) ... \( Z_n \) 为并联阻抗,如下图所示。
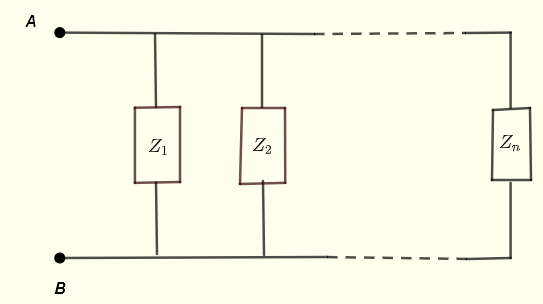
A和B点之间的等效阻抗为
\[ \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_1} + \dfrac{1}{Z_2} + ... + \dfrac{1}{Z_n} \]
示例 2
求下图所示并联RLC电路的复数阻抗,已知:
频率 \( f = 1.5 \; kHz \) , \( C = 15 \; \mu F \) , \( L = 20 \; mH \) 和 \( R = 50 \; \Omega \)

问题 2 的解决方案
设
\( Z_R = R \) , \( Z_C = \dfrac{1}{j \omega C} \) , \( Z_L = j \omega L\)
应用并联电路的阻抗规则
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_R} + \dfrac{1}{Z_C} + \dfrac{1}{Z_L} \)
\( = \dfrac{1}{R} + \dfrac{1}{\dfrac{1}{j \omega C}} + \dfrac{1}{j \omega L} \)
设
\( X_L = \omega L \) 和 \( X_C = \dfrac{1}{\omega C} \)
将上述结果重写为
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{1}{\dfrac{X_C}{j}} + \dfrac{1}{j X_L} \)
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{j}{{X_C}} - j \dfrac{1}{ X_L} \)
\( = \dfrac{1}{R} + j (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} ) \)
上述复数的模 \( r \) 为
\( r = \sqrt { (\dfrac{1}{R})^2 + (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} )^2} \)
其相位角 \( \alpha \) 为
\( \alpha = \arctan \left(\dfrac{\dfrac{1}{{X_C}} - \dfrac{1}{ X_L}}{\dfrac{1}{R}} \right) \)
\( = \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) \)
我们现在使用复数的指数形式来表示
\( \dfrac{1}{Z_{AB}} = r e^{j\alpha} \)
我们现在将等效阻抗 \( Z_{AB} \) 写成指数形式
\( Z_{AB} = \dfrac{1}{r} e^{-j \alpha} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{-j \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) } \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{j \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) } \)
我们现在使用已知数值
\( f = 1.5 \; kHz \) , \( C = 15 \; \mu F \) , \( L = 20 \; mH \) 和 \( R = 50 \; \Omega \)
\( X_L = \omega L = 2 \pi f L = 2 \pi 1.5 \times 10^3 \times 20 10^{-3 } = 188.50 \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{ 2\pi f C} = \dfrac{1}{ 2\pi 1.5 \times 10^3 \times 15 10^{-6}} = 7.07\)
模:\( \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{50}\right)^2 + \left(\dfrac{1}{{7.07}} - \dfrac{1}{ 188.50} \right)^2}} \)
\( = 7.27 \)
相位角:\( \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) \)
\( = \arctan \left(\dfrac{50}{188.50}-\dfrac{50}{7.07} \right) \)
\( = - 81.64^{\circ} \)
可以使用并联RLC电路阻抗计算器进行更多练习。