谐振串联RLC电路

目录

谐振 RLC串联电路 和谐振频率、截止频率的公式推导、带宽和品质因数的定义，并在例子中进行详细解答。 \( \) \( \) \( \) \( \)
在下文中，\( I \) 表示真实电流 \( i \) 的复数（极坐标）形式，\( V_i \) 表示真实电压 \( v_i \) 的复数（极坐标）形式。
可以使用谐振串联RLC电路计算器来验证下面例子的计算结果，并进一步练习和研究这些电路。

A - 谐振串联RLC电路

考虑下图所示的串联RLC电路。

对于由频率为 \( f \) 的电压源供电的电路，串联RLC电路的总阻抗 \( Z \) 表示为：
\[ Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
电流 \( I \) 和电压 \( V_i \) 之间的关系为：
\[ I = \dfrac{V_i}{Z} \]
其中 \( V_i \) 和 \( I \) 分别是电压 \( v_i \) 和电流 \( i \) 的复数形式。
根据复数的模的定义，模 \( |Z| \) 表示为：
\( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \)
如果 \( V_0 \) 是电压源 \( v_i = V_0 \cos (\omega t) \) 的峰值，那么电流 \( I \) 的峰值 \( I_0 \) 表示为：
\( I_0 = \dfrac{V_0}{ |Z| } = \dfrac{V_0}{ \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} } \)
谐振频率 定义为 \( I_0 \) 最大或 \( Z \) 模最小时的频率。
由于电阻 \( R \) 不随频率变化，因此 \( |Z| \) 的最小值发生在 \( \omega = \omega_r \)，即：
\( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \)
求解上式得出谐振频率：
\[ \omega_r = \dfrac{1}{\sqrt {L C}} \quad \quad (I) \]
在谐振频率 \( \omega = \omega_r \) 下，我们有：
1) \( Z = R \)
对于电压源 \( v_i \) 的峰值 \( V_0 \)，电流 \( I \) 的峰值 \( I_0 \) 表示为：
2) \( I_0 = \dfrac{V_0}{R} \)
设 \( X_L = \omega L \) 和 \( X_C = \dfrac{1}{\omega C} \)
3) \( X_L = X_C \)

例子 1
在上述RLC串联电路中，设 \( R=300 \; \Omega \)、\( L = 100 \; mH \)、\( C = 100 \mu F \)。
a) 求谐振频率 \( \omega_r \)
b) 绘制 \( |Z| \)、\( X_L = \omega L \)、\( X_C = \dfrac{1}{\omega C} \) 和 \( I_0 \) 随频率 \( \omega \) 变化的图，并讨论所得图形。

例子 1 解决方案
a)
谐振频率 \( \omega_r \) 表示为：
\( \omega_r = \dfrac{1}{\sqrt {L C}} = \dfrac{1}{\sqrt{100\times10^{-3} \times 100 \times 10^{-6}}} \approx 316.23\)
b)
下图展示了 \( |Z| \)、\( X_L \) 和 \( X_C \) 的图形。
从图中可以看出，\( |Z| \) 的最小值等于 \( R = 300 \; \Omega \)（A点）
\( X_L \) 和 \( X_C \) 的图形相交（B点），因此 \( X_L = X_C \) 或 \( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \) 。



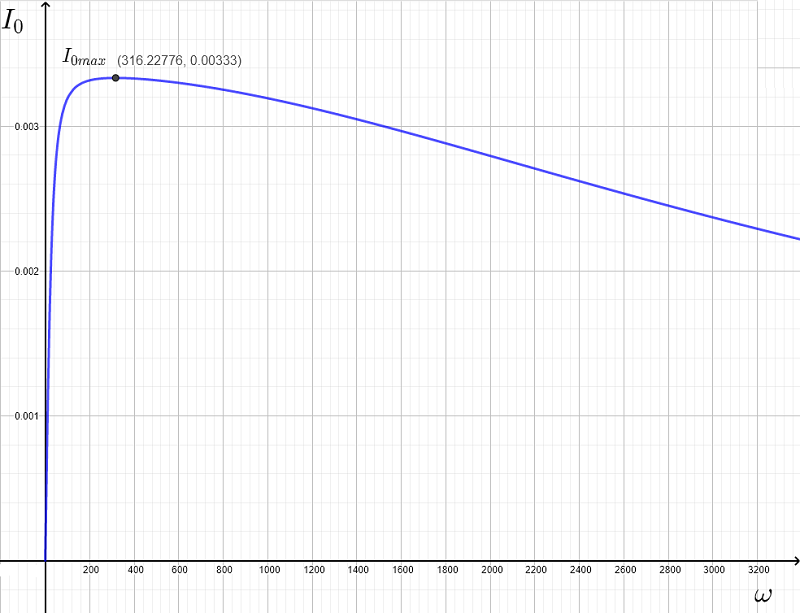
下图展示了电流 \( I_0 \)，并且在谐振频率 \( \omega_r \approx 316.23\) 时达到最大值（四舍五入至小数点后两位）。

B - 谐振电路中的平均功率

平均功率 \( P_a \) 传递到串联RLC电路的公式为： \[ \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 |Z|} \cos \theta \quad \quad (II) \] 其中 \( \theta \) 是阻抗 \( Z = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \) 的辐角，表示为：
\( \theta = \arctan \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
使用反三角函数性质，我们有：
\( \tan \theta = \left( \dfrac{ \omega L - \dfrac{1}{\omega C} }{R} \right) \)
\( \theta \) 可以看作是下面直角三角形的锐角。（使用直角三角形中角的正切定义，你可以得到与上述相同的 \( \tan \theta \)）。



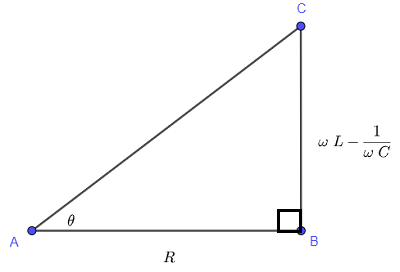
我们现在使用相同的三角形计算功率因数 \( \cos \theta \)
三角形的斜边计算如下：
\( AC = \sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2} \)
\( \cos \theta = \dfrac{AB}{AC} = \dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
将 \( \cos \theta \) 和 \( |Z| \) 代入上面的公式 (II)，并将功率 \( P_a \) 表示为：
\( \displaystyle \quad \quad P_a = \dfrac{V_0^2}{2 \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} }\dfrac{R}{\sqrt {R^2 + \left( \omega L - \dfrac{1}{\omega C} \right)^2}} \)
简化：
\[ \displaystyle \quad \quad P_a = \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega L - \dfrac{1}{\omega C} \right)^2} \right) } \quad \quad (III) \]
在谐振频率 \( \omega_r = \dfrac{1}{\sqrt {LC}} \) 下，\( \left(\omega_r L - \dfrac{1}{\omega_r C} \right) = 0 \)，因此功率达到最大值： \[ P_{a max} = \dfrac{V_0^2}{2 \; R} \quad \quad (IV) \]

C - 谐振电路的截止频率和品质因数

我们现在定义截止频率 \( \omega_c \)，即在 (III) 式中功率 \( P_a(\omega) \) 为最大功率 \( P_{a max} \) 的一半 \( P_{a max} \) 在 (IV) 式中。
因此我们需要解方程：
\( P_a (\omega_c ) = \dfrac{1}{2} \left(\dfrac{V_0^2}{2 \; R} \right) \)

\( \dfrac{V_0^2 R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{2} \dfrac{V_0^2}{2 \; R} \)
简化为：
\( \dfrac{ R}{2 \left({R^2 + \left(\omega_c L - \dfrac{1}{\omega_c C} \right)^2} \right) } = \dfrac{1}{4 R} \)
交叉相乘，简化并将上述方程重写为：
\( (\omega_c L - \dfrac {1}{\omega_c C } ) = R^2 \)
通过提取平方根来求解，得到两个方程：
\( \omega_c L - \dfrac {1}{\omega_c C} = \pm R \)
将所有项乘以 \( \omega_c C \) 并简化：
\( \omega_c^2 L C - 1 = \pm \omega_c R C \)
将其重写为标准形式的二次方程：
\( \omega_c^2 L C \pm \omega_c R C - 1 = 0\)
解第一个二次方程 \( \quad \omega_c^2 L C + \omega_c R C - 1 = 0\)
得到两个解：
\( \omega_{c1} = \dfrac {- R C \pm \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

解第二个二次方程 \( \quad \omega_c^2 L C - \omega_c R C - 1=0\)
得到两个解：
\( \omega_{c2} = \dfrac {R C \pm \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
我们总共有四个解。注意，量 \( \sqrt{ (R C)^2 + 4 L C } \) 大于 \( RC \)，因此只有两个解有效，因为截止频率是正值。
截止频率 \( \omega_{c1} \) 和 \( \omega_{c2} \) 分别为：
\( \omega_{c1} = \dfrac {- R C + \sqrt{ (R C)^2 + 4 L C }}{ 2 L C } \)

\( \omega_{c2} = \dfrac {R C + \sqrt{ (R C)^2 + 4 L C}}{ 2 L C } \)
我们已经找到了谐振频率 \( \omega_r = \dfrac{1}{\sqrt{LC}} \)
使用简单代数将 \( \omega_{c1} \) 和 \( \omega_{c2} \) 重新写成 \( \omega_r \) 的形式：
\[ \omega_{c1} = - \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (V) \]
\[ \omega_{c2} = \dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \quad \quad (VI) \]

注意：
\[ \omega_{c1} \times \omega_{c2} = \omega_r^2 \quad \quad (VII) \]

谐振电路的带宽定义为：\( \Delta \omega = \omega_{c2} - \omega_{c1} \)

品质因数 \( Q \) 定义为：
\( Q = \dfrac{\omega_r}{\Delta \omega} \)
代入：
\( Q = \dfrac {\omega_r} { \left(\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} - \left(-\dfrac{R}{2 L} + \sqrt{ \left(\dfrac{R}{2 L}\right)^2 + \omega_r^2} \right) \right)} \)
简化：
\[ Q = \omega_r \dfrac{L}{R} \quad \quad (VIII) \]

D - 带详细解答的更多例子

例子 3
设计一个串联RLC谐振电路，使其具有下限截止频率 \( f_{c_1} = 650 \) 赫兹和上限截止频率 \( f_{c_2} = 950 \) 赫兹。
a) 如果电阻 \( R \) 为 \( 30 \Omega \)，计算电容器 \( C \) 的电容和电感器 \( L \) 的电感。
b) 该电路的品质因数是多少？

例子 3 解决方案
a)
计算角频率：
\( \omega_{c_1} = 2 \pi f_{c_1} = 1300 \pi \) rad/s
\( \omega_{c_2} = 2 \pi f_{c_1} = 1900 \pi \) rad/s
使用上面推导的公式 (VII)
\( \omega_{c_1} \times \omega_{c_2} = \omega_{r}^2 \) 计算电路的谐振频率 \( \omega_{r} \)。
\( \omega_{r} = \sqrt {\omega_{c_1} \times \omega_{c_2}} = \sqrt {1300 \pi \times 1900 \pi } = 100 \sqrt{247} \pi = 4937.400 \) rad/s
\( \omega_{c_2} - \omega_{c_1} = \dfrac{R}{L} \)
因此：
\( L = \dfrac{R } {\omega_{c_2} - \omega_{c_1}} = \dfrac{30} {1900 \pi - 1300 \pi } = 0.01591 \) H
\( \omega_{r} = \dfrac{1}{\sqrt {L C} } \)
因此：
\( C = \dfrac{1}{\omega_{r}^2 L} = \dfrac{1}{(100 \sqrt{247} \pi)^2 \times 0.01591} = 2.5783 \times 10^{-6} \) F

b)
品质因数为：
\( Q = \dfrac{\omega_{r}}{\omega_{c_2} - \omega_{c_1}} = \dfrac{100 \sqrt{247} \pi}{1900 \pi - 1300 \pi } = 2.62\)

更多参考资料和链接

• 谐振串联RLC电路计算器
• RLC串联电路
• 串联RLC电路阻抗计算器
• 并联RLC电路阻抗计算器
• RLC串联电流绘图计算器