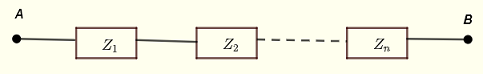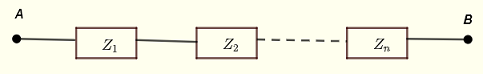交流电路中的阻抗公式

目录

串联阻抗

如图所示，阻抗 \( Z_{AB} \) 相当于串联的阻抗 \( Z_1 \)、\( Z_2 \) ... \( Z_n \)，公式为
\( Z_{AB} = Z_1 + Z_2 + ... + Z_n \)

并联阻抗

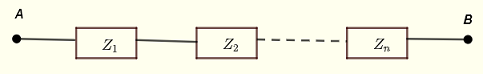
如图所示，阻抗 \( Z_{AB} \) 相当于并联的阻抗 \( Z_1 \)、\( Z_12 \) ... \( Z_n \)，公式为
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_1} + \dfrac{1}{Z_2} + ... + \dfrac{1}{Z_n} \)
或
\( Z_{AB} = \dfrac{1}{ \dfrac{1}{Z_1} + \dfrac{1}{Z_2} + ... + \dfrac{1}{Z_n} } \)

基本电路中的阻抗

电路	描述	阻抗 Z	幅值 |Z|	相位 \( \theta \)
	电阻	\( Z = R \)	\( |Z| = R \)	\( \theta = 0\)
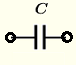
	电容	\( Z = \dfrac{1}{j \omega \; C} = - \dfrac{j}{\omega \; C} \)	\( |Z| = \dfrac{1}{\omega \; C} \)	\( \theta = - 90^{\circ}\) 或 \( -\dfrac{\pi}{2} \)
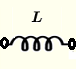
	电感	\( Z = j \omega \; L \)	\( |Z| = \omega \; L \)	\( \theta = 90^{\circ}\) 或 \(\dfrac{\pi}{2} \)
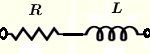
	串联 \( R \) 和 \( L \)	\( Z = R + j \omega \; L \)	\( |Z| = \sqrt{R^2 + (\omega \; L)^2} \)	\( \theta = \arctan \left(\dfrac{\omega \; L}{R}\right) \)
	并联 \( R \) 和 \( L \)	\( \dfrac{1}{Z} = \dfrac{1}{R} - j \dfrac{1}{\; \omega \; L} \)	\( |Z| = \dfrac{1}{\sqrt{\dfrac{1}{R^2}+\dfrac{1}{(\omega \; L)^2}} } \)	\( \theta = \arctan \left(\dfrac{R}{\omega \; L}\right) \)
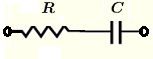
	串联 \( R \) 和 \( C \)	\( Z = R - j \dfrac{1}{\omega \; C} \)	\( |Z| = \sqrt{R^2 + \dfrac{1}{(\omega \; C)^2}} \)	\( \theta = \arctan \left(\dfrac{- 1}{R \omega C}\right) \)
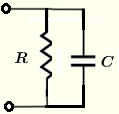
	并联 \( R \) 和 \( C \)	\( \dfrac{1}{Z} = \dfrac{1}{R} + j \; \omega \; C \)	\( |Z| = \dfrac{1}{\sqrt{\dfrac{1}{R^2}+(\omega \; C)^2} } \)	\( \theta = - \arctan \left( R {\omega \; C}\right) \)
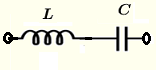
	串联 \( L \) 和 \( C \)	\( Z = j \omega L - j \dfrac{1}{\omega \; C} \)	\( |Z| = \left| \omega L - \dfrac{1}{\omega \; C} \right| \)	\( \theta = \begin{cases} \dfrac{\pi}{2}, & \mbox{如果 } \omega L - \dfrac{1}{\omega\; C } \gt 0 \\ - \dfrac{\pi}{2} , & \mbox{如果 } \omega L - \dfrac{1}{\omega \; C} \lt 0 \\ 0 , & \mbox{如果 } \omega L - \dfrac{1}{\omega \; C} = 0 \end{cases} \)
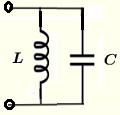
	并联 \( L \) 和 \( C \)	\( \dfrac{1}{Z} = j \; \omega \; C - \dfrac{j}{ \; \omega \; L} \)	\( |Z| = \dfrac{1}{\left| \omega C - \dfrac{1}{\omega \; L} \right|} \)	\( \theta = \begin{cases} -\dfrac{\pi}{2}, & \mbox{如果 } \omega C - \dfrac{1}{\omega\; L} \gt 0 \\ \dfrac{\pi}{2} , & \mbox{如果 } \omega C - \dfrac{1}{\omega \; L} \lt 0 \\ 0, & \mbox{如果 } \omega C - \dfrac{1}{\omega \; L} = 0 \end{cases} \)
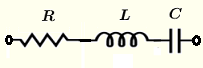
	串联 \( R \)、\( L \) 和 \( C \)	\( Z = R + j \omega \; L - j \dfrac{1}{\omega \; C}\)	\( |Z| = \sqrt{R^2 + \left(\omega \; L- \dfrac{1}{\omega \; C} \right)^2} \)	\( \theta = \arctan \left(\dfrac{\omega^2 L C - 1 }{ R \omega C}\right) \)
	并联 \( R \)、\( L \) 和 \( C \)	\( \dfrac{1}{Z} = \dfrac{1}{R} + j \omega \; C - j \dfrac{1}{ \omega \; L} \)	\( |Z| = \dfrac{1} { \sqrt{\dfrac{1}{R^2} + \left(\omega \; C- \dfrac{1}{\omega \; L} \right)^2 }} \)	\( \theta = - \arctan \left(\dfrac{R(\omega^2 \; L \; C - 1) }{ \omega \; L}\right) \)

更多参考资料和链接