串联RLC电路中的电流和电压计算

目录

本文讨论了如何使用复数阻抗来分析串联RLC电路中的电流和电压。复数极大地简化了交流电路中阻抗、电流和电压的计算。
由于符号 \( i \) 用于交流电路中的电流，这里我们使用 \( j \) 作为虚数单位，定义为 \( j^2 = -1 \) 或 \( j = \sqrt{-1} \)。
小写字母用于表示实际量的电流和电压。大写字母用于表示极坐标形式的复数量电流和电压。

A - 串联RLC电路中的复数阻抗和相量

对于由频率为 \( f \) 的电压源供电的电路，不同RLC元件的阻抗如下：
电阻 \( R \) 的复数形式阻抗 \( Z_R \) 为 \[ Z_R = R \] 电感 \( L \) 的复数形式阻抗 \( Z_L \)，也称为感抗，为 \[ Z_L = j \omega L \] 电容 \( C \) 的复数形式阻抗 \( Z_C \)，也称为容抗，为 \[ Z_C = - \dfrac{1}{\omega C} j \] 其中 \( \omega = 2 \pi f \)
最重要的是要注意感抗和容抗取决于电源电压的频率。

设 \( V_i \)、\( I \)、\( V_R \)、\( V_L \) 和 \( V_C \) 为 \( v_i \)、\( i \)、\( v_R \)、\( v_L \) 和 \( v_C \) 的复数形式。
应用扩展到复数阻抗的基尔霍夫电压定律，写成
\( V_i - V_R - V_L - V_C = 0\)     (1)
应用扩展到复数阻抗的欧姆定律，写成
\( V_R = Z_R I \)
\( V_L = Z_L I \)
\( V_C = Z_C I \)
将上述公式代入方程 (1)，得到
\( V_i = Z_R I + Z_L I + Z_C I = 0\)
解出 \( I \)
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
设 \( Z \) 为串联RLC电路的等效复数阻抗，定义为
\[ Z = Z_R + Z_L + Z_C = R + j \left(\omega L - \dfrac{1}{\omega C} \right) \]
\( Z \) 的模数为 \[ |Z| = \sqrt{R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \]
\( Z \) 的幅角为 \[ \theta = arctan \left( \dfrac {\omega L - \dfrac{1}{\omega C}}{R} \right) \]
注意阻抗 \( Z \) 的模数和幅角都依赖于电源电压的频率（\( \omega = 2 \pi f \)）。这一特性在滤波器设计中非常有用，并且在电子电路中有许多其他应用。
将 \( Z \) 写成极坐标形式
\[ Z = |Z| \; \angle \; \theta \]
上面得到的 \( Z_R, Z_L, Z_C \) 和 \( Z \) 的表达式可以使用相量进行几何解释，如下图所示。


在部分 (a) 中，\( Z_R, Z_L\) 和 \( Z_C \) 被绘制在以实部为水平轴、虚部为垂直轴的坐标系中。
在部分 (b) 中，使用向量（或复数）加法几何绘制了 \( Z = Z_R + Z_L + Z_C \)。
在部分 (c) 中，一个直角三角形的斜边表示 \( Z \) 的模数：使用勾股定理：\( |Z| = \sqrt {R^2 + \left(\omega L - \dfrac{1}{\omega C}\right)^2} \)，这与上面使用复数得到的结果完全一致。
再次使用直角三角形，角度：\( \theta = \arctan \left (\dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)

B - 串联RLC电路的电流和电压

设 \( v_i = V_0 \cos ( \omega t) \)，\( V_0 \) 为电源电压的峰值。
欧拉公式
\( e^{j \omega t} = \cos (\omega t) + j \sin (\omega t )\)
因此 \( v_i \) 也可以写成
\( v_i \) 等于 \( e^{j \omega t} \) 的实部。
现在我们省略“实部”并在复数中进行所有计算，将 \( V_i \) 定义为复数形式
\( V_i = V_0 e^{j \omega t} \)
并推导出复数形式的 \( I \)
\( I = \frac{V_0 e^{j\omega t}}{|Z| \; \angle \; \theta} \)
极坐标形式的 \( I \) 为
\( I = \dfrac{V_0}{|Z|} \; \angle \; \omega t - \theta \)
\( I = I_0 \; \angle \; \omega t - \theta \)，其中 \( I_0 = \dfrac{V_0}{|Z|} \)
将阻抗 \( Z_R, Z_L\) 和 \( Z_C \) 重写为极坐标形式
\( Z_R = R = R \; \angle \; 0 \)
\( Z_L = j \omega L = \omega L \; \angle \; \pi/2\)
\( Z_C = - \dfrac{1}{\omega C} j = \dfrac{1}{\omega C} \; \angle \; - \pi/2\ \)
电压为
\( V_R = Z_R I = (R \; \angle \; 0) (I_0 \; \angle \; {\omega t - \theta}) = R I_0 \angle \; \omega t - \theta \)
\( V_L = Z_L I = (\omega L \; \angle \; \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \omega L I_0 \; \angle \; {\omega t - \theta + \pi/2} \)
\( V_C = Z_C I = (\dfrac{1}{\omega C} \; \angle \; - \pi/2) (I_0 \; \angle \; {j\omega t - \theta}) = \dfrac{I_0}{\omega C} \; \angle \; {\omega t - \theta - \pi/2} \)
电流 \( I \) 和电压 \( V_R \) ，\( V_C \) 和 \( V_C \) 如下图所示使用相量表示。

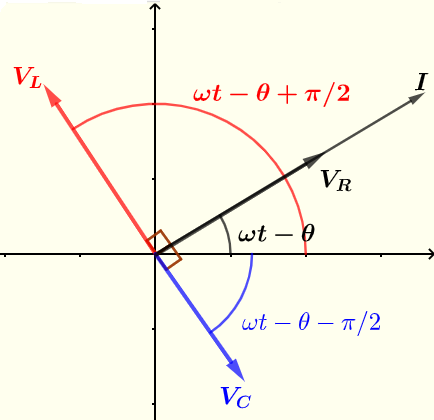
实际电流和电压是通过计算上述复数（或极坐标）形式的电流和电压的实部得出的。
\( i = \dfrac{V_0}{|Z|} \cos( \omega t - \theta) \)

\( v_R = R \dfrac{V_0}{|Z|} \cos(\omega t - \theta) \)

\( v_L = \omega L \dfrac{V_0}{|Z|} \cos(\omega t - \theta + \pi/2) \)

\( v_C = \dfrac{V_0}{\omega C|Z|} \cos(\omega t - \theta - \pi/2) \)

注意 在计算过程中可以省略时间变化 \( \omega t \)，如果需要将电流和电压写成时间的函数，则可以在最后加上时间变化。下面的示例展示了忽略时间依赖性如何分析RLC电路。

C - 带有详细解答的示例

示例 1
在一个串联RLC电路中，电源电压为 \( v_i = 20 \cos (\omega t) \)，其中 \( \omega = 1000 \; rad/s \)，电容器的电容 \( C = 200 \; \mu F \)，电感器的电感 \( L = 400 \; mH\) 和电阻器的电阻 \( R = 400 \; \Omega \)。
a) 计算电容、电感和电阻的阻抗以及串联RLC电路的等效阻抗 \( Z \) 的复数形式。
b) 计算电流和所有电压的复数形式。
c) 计算实际电流和电压。

示例 1 的解答
a)
电阻 \( R \) 的复数形式阻抗 \( Z_R \) 为
\( Z_R = R = 400 \; \Omega \)
电感 \( L \) 的复数形式阻抗 \( Z_L \)，也称为感抗，为
\( Z_L = j \omega L = j \cdot 1000 \cdot 400 \cdot 10^{-3} = 400 j \; \Omega \)
电容 \( C \) 的复数形式阻抗 \( Z_C \)，也称为容抗，为
\( Z_C = - \dfrac{1}{\omega C} j = - \dfrac{1}{1000 \cdot 200 \cdot 10^-6} j = - 5 j \; \Omega \)
\( Z = Z_R + Z_L + Z_C = 400 + 400 j - 5 j = 400 + 395 j \)
b)
\( v_i = 20 cos ( \omega t) \)，因此电源电压的极坐标形式 \( V_i = 20 \; \angle \; 0\)
我们已经看到电流的极坐标形式为
\( I = \dfrac{V_i}{Z_R + Z_L + Z_C } \)
代入已知量
\( I = \dfrac{20 \; \angle \; 0}{400 + 395 j}\)
将分母重写为极坐标形式
\( 400 + 395 j = \sqrt {400^2+395^2} \; \angle \; \arctan\left(\dfrac{395}{400}\right) = 562.16 \; \angle \; 44.64^{\circ} \)
计算 \( I \)
\( I = \dfrac{20 \; \angle \; 0}{562.16 \; \angle \; 44.64^{\circ}} = \dfrac{20}{562.16} \; \angle \; 0 - 44.64^{\circ} \)
简化
\( I = 0.0356 \; \; \angle \; - 44.64^{\circ} \) A
\( V_R = R I = 400 (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; - 44.64^{\circ}\) V
\( V_L = Z_L I = 400 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 14.24 \; V \; \angle \; 45.36^{\circ}\) V
\( V_C = Z_C I = - 5 j (0.0356 \; \; \angle \; - 44.64^{\circ}) = 0.18 \; V \; \angle \; -134.6^{\circ}\) V

示例 2
在一个串联RLC电路中，电源电压为 \( v_i = 10 \cos (\omega t) \)，电容器的电容 \( C = 200 \; \mu F \)，电感器的电感 \( L = 200 \; mH\) 和电阻器的电阻 \( R = 500 \; \Omega \)。
a) 计算阻抗 \( Z \) 的虚部为零时的角频率 \( \omega \)。
b) 计算在部分a中找到的频率下的电流和电压。

示例 2 的解答
a)
对于串联RLC电路 \( Z = R + j(\omega L - \dfrac{1}{\omega C} ) \)
当阻抗 \( Z \) 的虚部为零时
\( \omega L - \dfrac{1}{\omega C} = 0 \)
求解 \( \omega \)
\( \omega^2 L C = 1 \)
\( \omega = \dfrac{1}{\sqrt{L C}} \)
将 \( L \) 和 \( C \) 的数值代入
\( \omega = \dfrac{1}{ \sqrt{ 200\cdot10^{-3} \cdot 200 \cdot 10^{-6}}} = 158.11 \) rad/s
b)
\( I = \dfrac{V_i}{Z} = \dfrac{10 \; \angle \; 0}{R \; \angle \; 0} = \dfrac{10}{500} \; \angle \; 0 = 0.02 \; \angle\; 0 \)
\( V_R = R I = 500 \cdot 0.02 \; \angle \; 0 = 10 \; \angle\; 0 \)
\( V_C = Z_C I = \dfrac{1}{\omega C} \; \angle \; -90^{\circ} \cdot 0.02 \; \angle\; 0 = \dfrac{1}{\omega C} \cdot 0.02 \; \angle \; -90^{\circ} = \dfrac{1}{158.11 \cdot 200 \cdot 10^{-6}} \cdot 0.02 \; \angle \; -90^{\circ} = 0.6324 \; \angle \; -90^{\circ} \)
\( V_L = Z_L I = \omega L \; \angle \; 90^{\circ} \cdot 0.02 \; \angle\; 0 = \omega L \cdot 0.02 \; \angle \; 90^{\circ} = 158.11 \cdot 200 10^{-3} \cdot 0.02 \; \angle \; 90^{\circ} = 0.6324 \; \angle \; 90^{\circ} \)

示例 3
在一个串联RLC电路中，电源电压为 \( v_i = V_0 \cos (2 \pi f t) \)，其中 \( f \) 为频率，电容器的电容 \( C = 47 \; \mu F \)，电感器的电感 \( L = 100 \; mH\) 和电阻器的电阻 \( R = 200 \; \Omega \)。
a) 计算电容、电感和电阻串联时的总阻抗 \( Z \)，并写成极坐标形式 \( Z = |Z| \; \angle \; \theta \)
b) 求使 \( \theta = -60^{\circ} \) 的频率 \( f \)。

示例 3 的解答
a)
对于串联RLC电路 \( Z = R + j(\omega L - \dfrac{1}{\omega C}) \)
将已知量代入
\( Z = R + j(\omega L - \dfrac{1}{\omega C}) = 200 + j( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})\)
\( Z = \sqrt {200^2 + ( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}})^2} \; \angle \; \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) \)
b)
\( \arctan \left(\dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200}\right) = -60^{\circ} \)
\( \dfrac{\omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}}}{200} = \tan (-60^{\circ}) = -1.73205 \)
将方程的各项乘以 \( 200 \) 以消去分母
\( \omega \cdot 100 \cdot 10^{-3} - \dfrac{1}{\omega \cdot 47 \cdot 10^{-6}} = -346.41 \)
将方程的各项乘以 \( \omega \cdot 47 \cdot 10^{-6} \) 以消去分母
\( 47 \cdot 10^{-7} \omega^2 - 1 = -0.01628127 \omega \)
求解以上二次方程 \( \omega \)，选择正解。
\( \omega = 53.23 \) rad/s
\( \omega = 2 \pi f = 60.3682 \)
\( f = \dfrac{60.3682}{2 \pi} = 9.60789 \) Hz

示例 4
在一个串联RLC电路中，电源电压为 \( v_i = V_0 \cos (2 \pi f t) \)，电容器的电容 \( C = 470 \mu \)F，电感器的电感 \( L = 50 \)mH，电阻器的电阻为 \( R \)。
a) 计算电容、电感和电阻串联时的总阻抗 \( Z \)，并写成极坐标形式 \( Z = |Z| \; \angle \; \theta \)
b) 求使 \( \theta = 40^{\circ} \) 并且 \( |Z| = 100 \) 的电阻 \( R \) 和频率 \( f \)。

示例 4 的解答
a)
对于串联RLC电路 \( Z = R + j(\omega L - \dfrac{1}{\omega C}) \)
将 \( Z \) 写成极坐标形式
\( Z = \sqrt{R^2 + (\omega L - \dfrac{1}{\omega C})^2} \; \angle \; \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) \)
b)
\( \theta = \arctan \left( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} \right) = 40^{\circ} \)
\( \dfrac{\omega L - \dfrac{1}{\omega C}}{R} = \tan 40^{\circ} = 0.83909\)
\( \omega L - \dfrac{1}{\omega C} = 0.83909 R \)
将上述代入 \( |Z| \)
\( \sqrt{R^2 + (0.83909 R)^2} = 100 \)
求解 \( R \)
\( R = 76.6048 \; \Omega \)
\( \omega L - \dfrac{1}{\omega C} = 0.83909 R = 64.27832 \)
求解 \( \omega \)
\( \omega = 1317.8557 \) rad/s
\( f = \dfrac{1317.8557}{2\pi} = 209.74324 \) Hz

更多参考资料和链接