在交流电路中使用复数

目录

本文讨论了如何使用复数来分析和计算交流电（AC）电路中的电流和电压，以及如何用复数表示电阻、电容器的阻抗和电感器的阻抗。还展示了如何通过使用复数阻抗来应用类似于欧姆定律的数学模型来建模交流电路。
使用复数来建模交流电路以及其他工程领域中许多正弦波现象的主要原因有两个：
1) 交流信号（以及许多其他正弦波现象）具有一个幅值和一个相位，它们分别与复数的模和幅角非常相似。
2) 复数的基本运算，如加法、减法、乘法和除法，更容易执行和编程。
注意
1) 因为符号 \( i \) 在交流电路中用于表示电流，这里我们用 \( j \) 作为虚数单位，定义为 \( j^2 = -1 \) 或 \( j = \sqrt{-1} \)。
2) 符号 \( \Re e\) 代表复数的实部。

A - 复数的实部

标准形式的复数 \( Z = a + j b \) 可以写成指数形式如下：
\( \displaystyle Z = r e^{j \theta} \)      其中 \( j^2 = -1 \)
也可以写成极坐标形式如下：
\( Z = r \angle \theta \)
其中 \( r = \sqrt{a^2 +b^2} \) 是 \( Z \) 的模，而 \( \tan \theta = \dfrac{b}{a} \) 是它的幅角。
取指数形式复数两边的实部，记作 \( \Re e \)：
\( \Re e (r e^{j \theta}) = \Re e (r ( \cos \theta + j \sin \theta )) = \Re e (r \cos \theta + j r \sin \theta ) = r \cos \theta \)
在接下来的内容中，\( \Re e \) 表示给定复数的实部。

B - 单变量复函数的导数

设 \( f(t) \) 是一个单变量 \( t \) 的复函数，可以写成如下形式：
\( f(t) = a(t) + j b(t) \)
其中 \( a(t) \) 是 \( f(t) \) 的实部，\( b(t) \) 是 \( f(t) \) 的虚部，\( j = \sqrt {-1}\) 是虚数单位。
设 \( f'(t) \) 是 \( f(t) \) 关于 \( t \) 的一阶导数，定义为：
\( f'(t) = \lim_{h\to 0} \dfrac{f(t+h) - f(t) }{h} \)
将 \( f(t+h) \) 替换为 \( a(t+h) + j b(t+h) \)：
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) + j b(t+h) - (a(t) + jb(t))}{h} \)
分离项得到：
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) - a(t)}{h} + j \lim_{h\to 0} \dfrac{ j b(t+h) - jb(t))}{h} \)
\( f'(t) = a'(t) + j b'(t) \)
现在容易证明，复函数 \( f(t) \) 的导数的实部等于 \( f(t) \) 的实部的导数，可以写成：
\( \Re e(f'(t)) = a'(t) = (\Re e(f(t))' \)
或
\( \Re e \left ( \dfrac{df(t)}{dt} \right) = \dfrac {d a(t)}{dt} = \dfrac {d \left (\Re e(f(t)) \right)}{dt} \)

C - 单变量复函数的积分

设 \( f(t) \) 是一个单变量 \( t \) 的复函数，可以写成如下形式：
\( f(t) = a(t) + j b(t) \)
其中 \( a(t) \) 是 \( f(t) 的实部，\( b(t) \) 是 \( f(t) 的虚部，\( j = \sqrt {-1}\) 是虚数单位。
设 \( F(t) \) 是由不定积分定义的函数：
\( \displaystyle F(t) = \int f(t) dt = \int (a(t) + j b(t)) dt = \int a(t) dt + j \int b(t) dt \)
现在容易证明，复函数 \( f(t) \) 的不定积分的实部等于 \( f(t) 的实部的不定积分，可以写成：
\( \displaystyle \Re e \left( \int f(t) dt \right) = \int a(t) dt = \int \left( \Re e f(t) \right) dt \)

现在我们使用上述概念来分析使用复数的简单交流电路。

D - 交流电压源与复数

在接下来的内容中，\( v(t) \) 是一个随时间 \( t \) 变化的交流电压源，给定为：
\( v(t) = V_0 \cos(\omega t) \)
其中 \( V_0 \) 是峰值电压的实数，\( \omega = 2 \pi f \) 也是一个实数，\( f \) 是电压源的频率。
使用复数，\( v(t) \) 也可以写成：
\( v(t) = V_0 \cos(\omega t) = \Re e ( V_0 \cos(\omega t) + j V_0 \sin(\omega t) ) = \Re e (V_0 e^{j\omega t} ) \)

E - 交流电路中的电阻

让我们考虑一个简单的交流电路，其中有一个电阻，如下图所示。设 \( v(t) \) 是一个交流电压源，给定为：
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
其中 \( V_0 \) 和 \( \omega \) 是实数。


电阻 \( R \) 上的电流 \( i \) 和电压 \( v(t)_R \) 之间的关系为：
\( v(t)_R = R i \)
使用上图的单回路，有：
\( v(t) = v(t)_R \)
\( v(t) \) 由 \( v(t) = V_0 \cos(\omega t) \) 给定
因此：
\( v(t)_R = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
结合上述关系，我们写成：
\( R i = \Re e (V_0 e^{j\omega t} ) \)       (I)
设 \( V_R = V_0 e^{j\omega t} \)，并将上面的 (I) 重新写成：
\( R i = \Re e V_R \)
由于 \( R \) 是实数，上式可写为：
\( i = \Re e \left( \dfrac{V_R }{R} \right) \)
设 \( Z_R \) 为定义为电阻的阻抗，则：
\( Z_R = R \)
由于 \( R \) 是实数，电阻的阻抗 \( Z_R \) 是一个实数。
电流 \( i \) 可以写成：
\( i = \Re e \left( \dfrac{ V_R } {Z_R} \right) \)
设：
\( I = \dfrac{ V_R } {Z_R} \)
上式给出了类似于直流（DC）电路中欧姆定律的关系。复数量 \( I \)，\( V_R \) 和 \( R \) 之间的关系使得计算更加简便。
这简化了计算，即我们使用复数阻抗、电压和电流进行计算，然后取实部作为最终答案。

F - 交流电路中的电容器

让我们考虑一个简单的交流电路，其中有一个电容器，如下图所示。设 \( v(t) \) 是一个交流电压源，给定为：
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

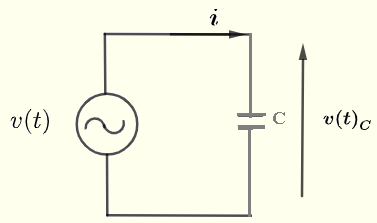
电容器 \( C \) 上的电流 \( i \) 和电压 \( v(t)_C \) 之间的关系为：
\( \displaystyle v(t)_C = \dfrac{1}{C} \int i dt \)
使用上图的单回路，有：
\( v(t) = v(t)_C \)
给定：
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
结合上述关系，我们写成：
\( \displaystyle \Re e (V_0 e^{j\omega t} ) = \dfrac{1}{C} \int i dt \)
对两边求导：
\( \displaystyle \dfrac{d}{dt} (\Re e (V_0 e^{j\omega t}) ) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
使用上面B部分讨论的结果，我们将上式重写为：
\( \displaystyle \Re e \dfrac{d}{dt} \left( V_0 e^{j\omega t} \right) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
简化后得到：
\( \Re e \left( j \omega V_0 e^{j\omega t} \right) = \dfrac{1}{C} i \)
由于电容 \( C \) 是实数，我们可以写成：
\( i = \Re e \left( j \omega C \; V_0 e^{j\omega t} \right) \)
设 \( V_C = V_0 e^{j\omega t} \)，并定义 \( Z_C \) 为电容器的复数阻抗，则：
\( Z_C = \dfrac{1}{j \omega C} = - \dfrac {j} { \omega C} \)
由于 \( C \) 是实数，电容器的阻抗 \( Z_C \) 是一个纯虚数。
电流 \( i \) 可以写成：
\( i = \Re e \left( \dfrac{ V_C } {Z_C} \right) \)
设：
\( I = \dfrac{ V_C } {Z_C} \)
上式类似于直流（DC）电路中的欧姆定律。复数量 \( I \)，\( V_C \) 和 \( Z_C \) 之间的关系使得计算更加简便。
这简化了计算，即我们使用复数阻抗、电压和电流进行计算，然后取实部作为最终答案。

G - 交流电路中的电感器

让我们考虑一个简单的交流电路，其中有一个电感器，如下图所示。设 \( v(t) \) 是一个交流电压源，给定为：
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

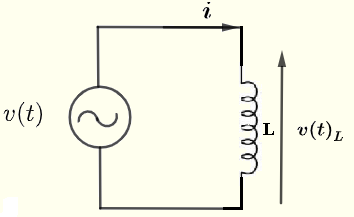
电感 \( L \) 上的电流 \( i \) 和电压 \( v(t)_L \) 之间的关系为：
\( v(t)_L = L \dfrac {d i}{ dt} \)
使用上图的单回路，有：
\( v(t) = v(t)_L \)
给定：
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
结合上述关系，我们写成：
\( \Re e (V_0 e^{j\omega t} ) = L \dfrac {d i}{ dt} \)
对两边求不定积分：
\( \displaystyle \int \Re e (V_0 e^{j\omega t}) dt = \int L \dfrac {d i}{ dt} dt \)
使用上面C部分讨论的结果，我们将上式重写为：
\( \displaystyle \Re e \int V_0 e^{j\omega t} dt = \int L \dfrac {d i}{ dt} dt \)
对两边求积分：
\( \Re e \left( \dfrac{1}{j\omega} V_0 e^{j\omega t} \right) = L i \)
由于电感 \( L \) 是实数，我们可以写成：
\( i = \Re e \left( \dfrac{1}{j \omega L} \; V_0 e^{j\omega t} \right) \)
设 \( V_L = V_0 e^{j\omega t} \) 并定义 \( Z_L \) 为电感器的阻抗，则：
\( Z_L = j \omega L \)
由于 \( L \) 是实数，电感器的阻抗 \( Z_L \) 是一个纯虚数。
电流 \( i \) 可以写成：
\( i = \Re e \left( \dfrac{ V_L } {Z_L} \right) \)
设：
\( I = \dfrac{ V_L } {Z_L} \)
上式给出了类似于欧姆定律的复数量 \( I \)，\( V_L \) 和 \( Z_L \) 之间的关系。
这简化了计算，即我们使用复数阻抗、电压和电流进行计算，然后取实部作为最终答案。

H - 结论：使用复数阻抗的欧姆定律

上文中，我们已经看到电阻、电容器和电感器的阻抗可以定义为纯实数或纯虚数的复数，具体如下：
1) 对于电阻 \( R\)；其阻抗为 \[ Z_R = R \] ，并且电流 \( I \)（复数形式）和电压 \( V_R \)（复数形式）之间的关系遵循交流电中的欧姆定律，表达为： \[ I = \dfrac{V_R}{Z_R} \] 2) 对于电容器 \( C \)；其阻抗为 \[ Z_C = -\dfrac{j}{\omega C} \] ，并且电流 \( I \)（复数形式）和电压 \( V_C \)（复数形式）之间的关系遵循交流电中的欧姆定律，表达为： \[ I = \dfrac{V_C}{Z_C} \] 3) 对于电感器 \( L \)；其阻抗为 \[ Z_L = j \omega L \] ，并且电流 \( I \)（复数形式）和电压 \( V_L \)（复数形式）之间的关系遵循交流电中的欧姆定律，表达为： \[ I = \dfrac{V_C}{Z_L} \] 我们得出结论，当使用复数来建模电阻、电容器和电感器的阻抗时，欧姆定律在交流电路中也是有效的。
还可以证明，当使用复数来建模电阻、电容器和电感器的阻抗时，基尔霍夫定律在交流电路中也是有效的。
串联和并联阻抗的等效阻抗可以使用类似于串联和并联电阻的规则来计算。

E - 带解答的示例

示例 1
求解电流 \( i \)、电阻 \( R \) 上的电压 \( v(t)_R \) 和电感 \( L \) 上的电压 \( v(t)_L \)，它们以 \( V_0 \)、\( R \)、\( L \) 和 \( \omega \) 表示，给定：
电压源：\( v(t) = V_0 \cos(\omega t) \)，\( \omega = 2 \pi f \)，其中 \( f \) 为频率。

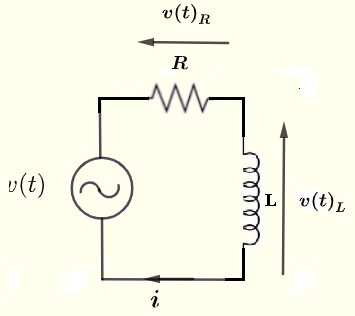
示例 1 的解答
设 \( V \) 是电压源 \( v(t) \) 的复数形式。
设 \( V_R \) 是电阻 R 上电压 \( v(t)_R\) 的复数形式。
设 \( V_L \) 是电感 L 上电压 \( v(t)_L\) 的复数形式。
设 \( I \) 是给定电路中通过电阻和电容的电流 \( i \) 的复数形式。
设电阻的复数阻抗为 \( Z_R = R \)，电感器的阻抗为 \(Z_L = j \omega L \)（见上文H部分）。
重绘电路图，定义上述复数量后，可以应用欧姆定律和基尔霍夫定律。

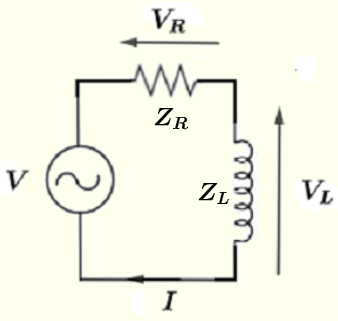
使用电路中单环路的基尔霍夫定律，有：
\( V = V_R + V_L \)         (I)
使用欧姆定律，将 \( V_R \) 和 \( V_L \) 重写为：
\( V_R = Z_R I \)
\( V_L = Z_L I \)
代入方程 (I)：
\( V = Z_R I + Z_L I = R I + j \omega L I = I(R + j \omega L ) \)
解出 \( I \)：
\( I = \dfrac{V}{R+j \omega L} \)         (II)
分母 \( R+j \omega L \) 是一个复数，可以写成复数形式为：
\( R+j \omega L = r e^{j\theta} \)
其中：
\( r = |Z| = \sqrt {R^2 + (L\omega)^2} \) 是模，
\( \theta = \arctan \left(\dfrac{\omega L}{R} \right) \) 是幅角，如下图所示的复平面所示。

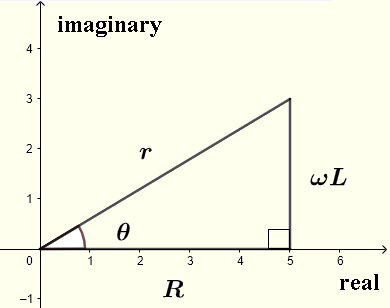
设 \( V = V_0 e^{j\omega t} \)
代入 \( V \) 和 \( R+j \omega L \) 的复数形式至 (II)，写成：
\( I = \dfrac{V_0 e^{j\omega t}}{r e^{j\theta}} \)
使用指数规则简化上述公式：
\( I = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
使用欧姆定律写成：
\( V_R = R I = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)

\( V_L = Z_L I = \dfrac{j V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
在 \( V_L \) 中，将 \( j \) 写成指数形式 \( j = e^{j \pi/2} \)：
\( V_L = \dfrac{ e^{j \pi/2} V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
使用指数规则重写上述公式为：
\( V_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \)
我们现在使用上述计算的复数量来计算 \( i \)，\( v(t)_R \) 和 \( v(t)_L \)，通过取实部如下：
\( i = \Re e I = \Re e \left( \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \)
结果为：
\[ i = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_R = \Re e V_R = \Re e \left( \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \) \[ v(t)_R = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_L = \Re e V_L = \Re e \left( \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \right) \) \[ v(t)_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t + \pi/2 -\theta) \]

更多参考资料和链接