Solve AC Circuits Problems with Solutions

Table of Contents

Kirchhoff's and Ohm's law is extended and used to solve AC circuits problems using impedances in complex forms.
All the quantities such as voltages, currents and impedances are represented by complex numbers in standard and polar forms.

Review of Complex Numbers

The imaginary unit is defined by \( j = \sqrt {-1} \) or \( j^2 = - 1 \)
A complex number \( Z \) in the standard the form \( Z = a + j b \) may be written in polar form as \[ Z = r \; \angle \; \theta \] where \( r \) and \( \theta \) are the modulus and argument , of \( Z \), respectively and are defined by \[ r = |Z| = \sqrt {a^2 + b^2} \; \text{and} \; \theta = \arctan \left( \dfrac{b}{a} \right) \; \text{within the range} \; -\pi \lt \theta \le \pi \] It is easier to divide or multiply complex numbers in polar form Let \[ Z_1 = r_1 \; \angle \; \theta_1 \; \text{and} \; Z_2 = r_2 \; \angle \; \theta_2 \] \[ Z_1 \cdot Z_2 = r_1 \cdot r_2 \; \angle \; \theta_1 + \theta_2 \] \[ \dfrac{Z_1}{Z_2} = \dfrac{r_1}{r_2} \; \angle \; \theta_1 - \theta_2 \]

Problems with Solutions

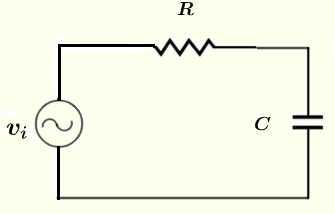
Problem 1
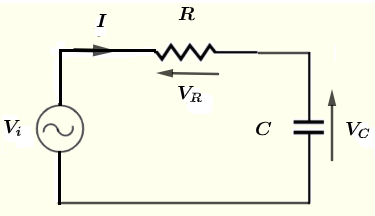
Find the magnitude and phase shift (polar form) of the current through and voltages across the resistor \( R \) and the capacitor \( C \) in the circuit below given that the voltage source \( v_i = 10 \cos (\omega t ) \) V, the resistances \( R = 100 \; \Omega \), \( C = 0.47 \; \mu F \), frequency \( f = 1 \) kHz and \( \omega = 2 \pi f \).

RC circuit in problem 1

Solution to Problem 1

Let \( V_i \), \( V_R \) \( V_C \) and \( I \) be the complex forms of \( v_i \), \( v_R \) \( v_C \) and \( i \) respectively.

RC circuit in problem 1

Use Kirchhoff's law of voltage around the loop to write the equation \[ V_i - V_R - V_C = 0 \text{(1)} \] The complex impedances of resistance \( R \) and capacitance \( C \) are given by \[ Z_R = R \; \quad \text{(real )}\] \[ Z_C = - j \dfrac{1}{\omega C} \; \quad \text{(imaginary)}\] Use Ohm's law to write \[ V_R = Z_R I \text{and} V_C = Z_C I \] Substitute \( V_R \) and \( V_C \) by their expression in equation (1) \[ V_i - Z_R I - Z_C I = 0 \] Solve the above for \( I \) \[ I = \dfrac{V_i}{Z_R + Z_C} \] Calculate \( V_R \) and \( V_C \) using Ohm's law as follows \[ V_R = Z_R I = \dfrac{V_i Z_R }{Z_R + Z_C} \] \[ V_C = Z_C I = \dfrac{V_i Z_C }{Z_R + Z_C} \] In complex polar form \( v_i = 10 \cos (\omega t ) \) may be written as
\[ V_i = 10 \; \angle \; 0 \] We now substitute \( V_i \), \( Z_R \) and \( Z_C \) by their expressions above to obtain \[ I = \dfrac{10 \; \angle \; 0}{R - j \dfrac{1}{\omega C}} \] \[ V_R = \dfrac{10 R \; \angle \; 0 \; }{R - j \dfrac{1}{\omega C}} \] \[ V_C = \dfrac{ (10 \; \angle \; 0 \;) (- j \dfrac{1}{\omega C}) }{R - j \dfrac{1}{\omega C}} \] Let the denominator to all the above expression be \( Z_D = R - j \dfrac{1}{\omega C} \) and rewrite it in complex form Modulus of \( Z_D \) : \[ | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} \] Argument of of \( Z_D \) : \[ \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-1}{R \omega C} \] We now rewrite the complex quantity \( - j \dfrac{1}{\omega C} \) in polar form \[ - j \dfrac{1}{\omega C} = \dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2} \] We now substitute all complex quantities in \( I \), \( V_R \) and \( V_C \) by their polar form and rewrite \[ I = \dfrac{10 \; \angle \; 0}{{ | Z_D | \; \angle \; \phi}} \] \[ V_R = \dfrac{10 R \; \angle \; 0 \; }{ | Z_D | \; \angle \; \phi} \] \[ V_C = \dfrac{10 \; \angle \; 0 \; (\dfrac{1}{\omega C} \; \angle \; -\dfrac{\pi}{2}) }{{ | Z_D | \; \angle \; \phi}} \] Simplify the above \[ I = \dfrac{10} { | Z_D | } \; \angle \; - \phi \] \[ V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi \] \[ V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi \] We now substitute all known quantities by their numerical values \[ \omega = 2 \cdot \pi \cdot f = 2 \cdot \pi 10^3 = 2000 \pi \] \[ | Z_D | = \sqrt {R^2 + \dfrac{1}{\omega^2 C^2}} = \sqrt {100^2 + \dfrac{1}{(2000 \pi)^2 (0.47 \cdot 10^{-6})^2}} = 353.08 \; \Omega \] \[ \phi = \arctan \dfrac{-\dfrac{1}{\omega C}}{R} = \arctan \dfrac{-\dfrac{1}{2000 \pi \cdot 0.47 \cdot 10^{-6} }}{100} = -73.55^{\circ} \] Hence \[ I = \dfrac{10} { | Z_D | } \; \angle \; - \phi = 0.0283 \; \angle \; 73.55^{\circ} \] Magnitude of \( I \) is \( 0.02832 \; A\) and phase shift is \( 73.55^{\circ} \) \[ V_R = \dfrac{10 R}{ | Z_D |} \; \angle \; - \phi = 2.832 \; \angle \; 73.55^{\circ} \] Magnitude of \( V_R \) is \( 2.832 \; V\) and phase shift is \( 73.55^{\circ} \) \[ V_C = \dfrac{10}{ \omega C | Z_D | } \; \angle \; -\dfrac{\pi}{2}- \phi = 9.591 \; \angle \; -16.45^{\circ} \] Magnitude of \( V_C \) is \( 9.591 \; V\) and phase shift is \( -16.45^{\circ} \)

Problem 2

Find the magnitude and phase shift (polar form) of the voltage \( v_o \) in the circuit below given that the voltage source \( v_i = 10 \cos (\omega t ) \; V \), the resistances \( R = 100 \; \Omega \), \( C = 0.47 \; \mu F \), \( L = 300 \; mH \) frequency \( f = 2 \) kHz and \( \omega = 2 \pi f \).

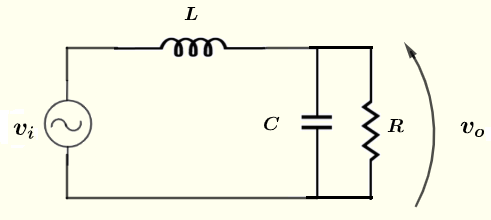
L C R circuit in Problem 2

Solution to Problem 2

Let \( I \), \( V_i \) and \( V_0 \) be the complex forms of \( i \) , \( v_i \) and \( v_o \) respectively \( V_i \) may be written in polar form as follows \[ V_i = 10 \; \angle \; 0 \] The impedances of resistor \( R \) is given by \[ Z_R = R \; \] The impedances of capacitance \( C \) is given by \[ Z_C = - j \dfrac{1}{\omega C} \] Resistor \( R \) and capacitor \( C \) are in parallel. The impedance \( Z \) that is equivalent to \( R \) and \( C \) is given by

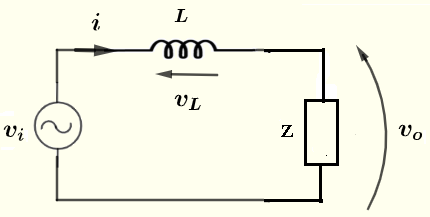
L C R circuit in problem 2 solution

\[ Z = \dfrac{Z_R \cdot Z_C}{Z_R + Z_C} \] The inductor \( L \) has complex impedance \( Z_L \) given by \[ Z_L = j \omega L \] Use Kirchhoff's law of voltage around the loop to write the equation \[ V_i - V_L - V_0 = 0 \quad \text{(1)} \] Use Ohm's law to write \[ V_L = Z_L I \quad \text{and} \quad V_0 = Z I \] Substitute \( V_L \) and \( V_0 \) by their expression in equation (1) \[ V_i - Z_L I - Z I = 0 \] Solve for \( I \) \( I = \dfrac{V_i}{ Z_L + Z} \) Use Ohm's law to write \[ V_o = Z I = \dfrac{Z}{ Z_L + Z} V_i\] Substitute by knwon quantities to find numerical values \[ \omega = 2 \pi f = 2 \pi \cdot 2000 = 4000 \pi \] \[ Z_R = R = 100 \] \[ Z_C = - j \dfrac{1}{\omega C} = - j \dfrac{1}{4000 \pi \cdot 0.47 \cdot 10^{-6}} = - 169.314 j \] \( Z = \dfrac{R \cdot Z_C}{R + Z_C} \) ( (\( R \) and \( C \) in Parallel ) \[ = \dfrac{100 \cdot (- 169.314 j)}{100 - 169.314 j } = 74.138 -43.787 j\] and \[ Z_L = j \omega L = 4000 \pi \cdot 300 \cdot 10^{-3} j = 3769.911 j \] \[ V_o = \dfrac{Z}{ Z_L + Z} V_i \] \[ = \dfrac{Z}{ Z_L + Z} V_i \] \[ = \dfrac{74.138 -43.787 j}{ 3769.911 j + 74.138 -43.787 j} V_i \] Simplify \[ = (-0.01135 -0.02012 j) V_i \] Write the complex number \( (-0.01135 -0.02012 j) \) in polar form and substitute \(V_i \) by its values in polar form given above. \[ = ( 0.02310 \angle -119.43^{\circ} ) (10 \; \angle \; 0) \] Simplify \[ V_o = 0.23 \; \angle \; -119.43^{\circ} \]

Problem 3

Find the magnitude and phase shift (polar form) of the voltage \( v_o \) in the circuit below given that the voltage source \( v_i = 10 \cos (\omega t ) \; V \), the resistances \( R_1 = 220 \; \Omega \), \( R_2 = 2.2 \; k\Omega \), \( R_3 = 1 \; k\Omega \), \( C_1 = 0.47 \; \mu F \), \( C_2 = 1.5 \; \mu F \), \( L = 30\; mH \) frequency \( f = 2.5 \) kHz and \( \omega = 2 \pi f \).

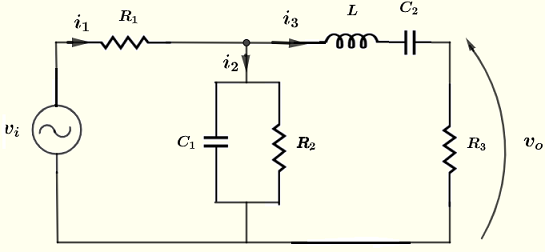
circuit in problem 3

Solution to Example 3

Let \( I_1 \), \( I_2 \), \( I_3 \), \( V_i \) and \( V_0 \) be the complex forms of \( i_1 \) , \( i_2 \), \( i_3 \) , \( v_i \) and \( v_o \) respectively. \( V_i \) may be written in polar form as follows \[ V_i = 10 \; \angle \; 0 \] \( V_o \) may be calculated using Ohm's law \[ V_o = R_3 I_3\] We therefore need to calculate \( I_3 \). Let us group the impedances, as shown in the circuit below, such that \[ Z_1 = R_1 \] \[ Z_2 = \dfrac{R_2 ( - \dfrac{1}{\omega C_1} j)}{R_2 - \dfrac{1}{\omega C_1} j} \] ( \( C_1 \) and \( R_2 \) are in parallel) \[ z_3 = R_3 + j \omega L - \dfrac{1}{ \omega C_2} j \] ( \( C_2 \), \( L \) and \( R_3 \) are in series)

circuit in problem 3

Kirchhoff's law of voltage applied to the two closed loops gives 2 equations \[ V_i - V_{z_1} - V_{z_2} = 0 \] \[ V_{z_2} - V_{z_3} = 0 \] Apply Ohm's law to write \( V_{z_1} = Z_1 I_1 \), \( V_{z_2} = Z_2 I_2 \) and \( V_{z_3} = Z_3 I_3 \) and substitute in the above equations to obtain equations including currents only. \[ V_i - Z_1 I_1 - Z_2 I_2 = 0 \quad \text{(1)} \]
\[ Z_2 I_2 - Z_3 I_3 = 0 \quad \text{(2)} \]
We now use Kirchhoff's law of current at the node A to write \[ I_1 = I_2 + I_3 \quad \text{(3)} \] We have 3 equations with three unknowns \( I_1 \), \( I_2 \) , and \( I_3 \), but we need only \(I_3\). Use equation (3) to substitute \( I_1 \) in equation (1) by \( I_2 + I_3 \) and hence eliminate \( I_1 \) from the equations and end up with a system of two equations and two unknowns. \[ V_i - Z_1 ( I_2 + I_3) - Z_2 I_2 = 0 \quad \text{(4)} \] \[ Z_2 I_2 - Z_3 I_3 = 0 \quad \text{(5)} \] Rewrite the above system of equations in standard form \[ (Z_1 + Z_2 ) I_2 + Z_1 I_3 = V_i \] \[ Z_2 I_2 - Z_3 I_3 = 0 \] Use determinant to solve the above system of equations \[ I_3 = \dfrac{\begin{vmatrix} Z_1 + Z_2 & V_i \\ Z_2 & 0 \end{vmatrix}}{\begin{vmatrix} Z_1 + Z_2 & + Z_1 \\ Z_2 & -Z_3 \end{vmatrix}} \] Evaluate the determinants to find \[ I_3 = \dfrac{Z_2}{(Z_1+Z_2)Z_3 + Z_1 Z_2} V_i \] Numerical Computations \[ \omega = 2 \pi f = 5000 \pi \] \[ Z_1 = 220 \] \[ Z_2 = \dfrac{2200 ( - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j)}{2200 - \dfrac{1}{5000 \pi \cdot 0.47 10^{-6}} j} = 8.30804 -134.93950 j \] \[ z_3 = 1000 + 5000 \pi \cdot 30 \cdot 10^{-3} j - \dfrac{1}{ 5000 \pi \cdot 1.5 \cdot 10^{-6}} j = 1000 + 428.79757 j \] \[ I_3 = (0.00013 - 0.00043 j)V_i = 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0\] \[ V_0 = R_3 I_3 = 1000 \cdot 0.00044 \angle -73.18^{\circ} \cdot 10 \angle 0 \] Simplify \[ V_0 = 4.4 \angle -73.18^{\circ} V \]

More Problems with Answers

Problem 4
Given \( v_i = 10 \angle 0^{\circ} \) , \( R = 200 \; \Omega \), \( C = 0.47 \; \mu F \), \( L = 40 \; mH \) , frequency \( f = 1 \) kHz, find the current \( I \) through and the voltage \( V_0 \) across the inductor in complex forms.

circuit in problem 4

Answer to Problem 4

Answer: \( I = 0.047 \angle -47.84^{\circ}\) , \(V_0 = 11.38 \angle 42.16^{\circ} \)

Problem 5
Given \( v_i = 10 \angle 0^{\circ} \) , \( R_1 = 100 \; \Omega \), \( C = 0.47 \; \mu F \), \( R_2 = 120 \; \Omega \), \( R_3 = 200 \; \Omega \), \( R_4 = 400 \; \Omega \), \( L = 20 \; mH \) , frequency \( f = 2 \) kHz, find the currents \( I_1 \), \( I_2 \) , \( I_3 \) and the voltages across each resistor in complex forms.
circuit in problem 5

Answer to Problem 5

Answers

Currents: \( I_1 = 0.054 \angle 10.55^{\circ} \; , \; I_2 = 0.048 \angle 23.01^{\circ} \; , \; I_3 = 0.013 \angle -42.22^{\circ} \)

Voltages: \( V_{R_1} = 5.49 \angle 10.55^{\circ} \; , \; V_{R_2} = 4.71 \angle -12.32^{\circ} \; , \; V_{R_3} = 2.60 \angle -42.22^{\circ} \; , \; V_{R_4} = 2.77 \angle 15.63^{\circ} \)

More References and Links