The equivalent impedance between points A and B is given by
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
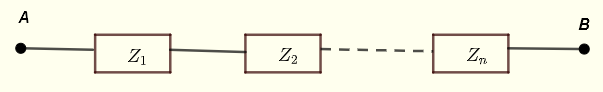
It is here discussed how complex impedances are used to compute the equivalent impedances to series and parallel impedances in AC circuits. All the steps are shown using symbolic calcualtions and then numerical values are used.
Because the symbol \( i \) is used for currents in AC circuits, here we use \( j \) as the imaginary unit defined by \( j^2 = -1 \) or \( j = \sqrt{-1} \)
Let \( Z_1 \) , \( Z_2 \) ... \( Z_n \) be impedances in series as shown below.
The equivalent impedance between points A and B is given by
\[ Z_{AB} = Z_1 + Z_2 + ... + Z_n\]
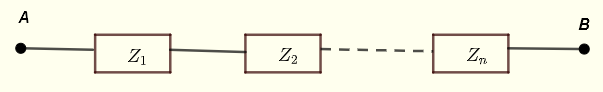
Example 1
Find the complex impedance equivalent to the series RLC circuit shown below given:
Frequency \( f = 1 \; kHz \) , \( C = 10 \; \mu F \) , \( L = 10 \; mH \) and \( R = 100 \; \Omega \)
Solution to Problems 1
Let
\( Z_R = R \) , \( Z_C = \dfrac{1}{j \omega C} = \dfrac{-j}{\omega C} \) , \( Z_L = j \omega L\)
Apply the rule of impedances of a series circuits
\( Z_{AB} = Z_R + Z_C + Z_L = R - \dfrac{j}{\omega C} + j \omega L \)
Let
\( X_L = \omega L = 2 \pi f L \) and \( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} \)
and rewrite \( Z_{AB} \) as follows
\( Z_{AB} = R + j(X_L - X_C) \)
Substitute with numerical values
\( X_L = \omega L = 2 \pi f L = 2 \pi 10^3 10^{-2} = 62.83 \Omega \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} = \dfrac{1}{2 \pi 10^3 10^{-5} } = 15.92 \Omega \)
Group imaginary terms
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) \)
Simplify
\( Z_{AB} = 100 + j ( 62.83 - 15.92 ) = 100 + 46.91 j\)
Write the above in exponential form
\( Z_{AB} = \sqrt {100^2 + 46.91^2} e^{j \arctan{\dfrac{46.91}{100}}} = 110.45 e^{j 0.44} \)
\( Z_{AB} \) written in phasor form
\( Z_{AB} = 110.45 \angle 0.44 \; rad = 110.45 \angle 25.13^{\circ} \)
A series RLC circuit impedance calculator may be used for more practices.
Let \( Z_1 \) , \( Z_2 \) ... \( Z_n \) be impedances in parallel as shown below.
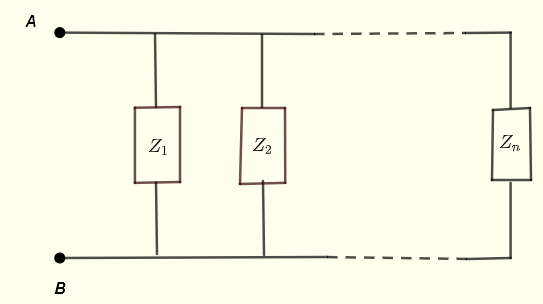
The equivalent impedance between points A and B is given by
\[ \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_1} + \dfrac{1}{Z_2} + ... + \dfrac{1}{Z_n} \]
Example 2
Find the complex impedance equivalent to the parallel RLC circuit shown below given:
Frequency \( f = 1.5 \; kHz \) , \( C = 15 \; \mu F \) , \( L = 20 \; mH \) and \( R = 50 \; \Omega \)
Solution to Problems 2
Let
\( Z_R = R \) , \( Z_C = \dfrac{1}{j \omega C} \) , \( Z_L = j \omega L\)
Apply the rule of impedances of a parallel circuits
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{Z_R} + \dfrac{1}{Z_C} + \dfrac{1}{Z_L} \)
\( = \dfrac{1}{R} + \dfrac{1}{\dfrac{1}{j \omega C}} + \dfrac{1}{j \omega L} \)
Let
\( X_L = \omega L \) and \( X_C = \dfrac{1}{\omega C} \)
and rewrite the above as
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{1}{\dfrac{X_C}{j}} + \dfrac{1}{j X_L} \)
\( \dfrac{1}{Z_{AB}} = \dfrac{1}{R} + \dfrac{j}{{X_C}} - j \dfrac{1}{ X_L} \)
\( = \dfrac{1}{R} + j (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} ) \)
The moduls \( r \) of the above complex number is given by
\( r = \sqrt { (\dfrac{1}{R})^2 + (\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} )^2} \)
and its argument \( \alpha \) is given by
\( \alpha = \arctan \left(\dfrac{\dfrac{1}{{X_C}} - \dfrac{1}{ X_L}}{\dfrac{1}{R}} \right) \)
\( = \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) \)
We now use the exponential form of complex number to write
\( \dfrac{1}{Z_{AB}} = r e^{j\alpha} \)
We now write the equivalent impedance \( Z_{AB} \) as a complex number in exponential form
\( Z_{AB} = \dfrac{1}{r} e^{-j \alpha} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{-j \arctan \left(\dfrac{R}{X_C}-\dfrac{R}{X_L} \right) } \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} e^{j \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) } \)
We now use the given values
\( f = 1.5 \; kHz \) , \( C = 15 \; \mu F \) , \( L = 20 \; mH \) and \( R = 50 \; \Omega \)
\( X_L = \omega L = 2 \pi f L = 2 \pi 1.5 \times 10^3 \times 20 10^{-3 } = 188.50 \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{ 2\pi f C} = \dfrac{1}{ 2\pi 1.5 \times 10^3 \times 15 10^{-6}} = 7.07\)
Moduls: \( \dfrac{1}{\sqrt { \left(\dfrac{1}{R}\right)^2 + \left(\dfrac{1}{{X_C}} - \dfrac{1}{ X_L} \right)^2}} \)
\( = \dfrac{1}{\sqrt { \left(\dfrac{1}{50}\right)^2 + \left(\dfrac{1}{{7.07}} - \dfrac{1}{ 188.50} \right)^2}} \)
\( = 7.27 \)
Argument: \( \arctan \left(\dfrac{R}{X_L}-\dfrac{R}{X_C} \right) \)
\( = \arctan \left(\dfrac{50}{188.50}-\dfrac{50}{7.07} \right) \)
\( = - 81.64^{\circ} \)
A parallel RLC circuit impedance calculator may be used for more practices.