Use Complex Numbers in AC circuits

Table of Contents

It is here discussed how complex numbers may be used to analyze and compute currents and voltages in AC (alternating current) circuits and also how the resistance, the impedance of a capacitor and the impedance of an inductor are represented by complex numbers. It is also shown how the use of complex impedances allows the use of a law similar to Ohm's law in order to mathematically model AC circuits.
Two main reasons that make the use of complex numbers suitable to model AC circuits, and many other sine wave phenomena in several branches of engineering, are:
1) the AC signals (and many other sine wave phenomena) are characterized by a magnitude and a phase that are, respectively, very similar to the modulus and argument of complex numbers.
2) the basic operations such as addition, subtraction, multiplication and division of complex numbers are easier to carry out and to program on a computer.
Note
1) Because the symbol \( i \) is used for currents in AC circuits, here we use \( j \) as the imaginary unit defined by \( j^2 = -1 \) or \( j = \sqrt{-1} \)
2) The symbol \( \Re e\) represents the real part of a complex number.

A - Real Part of Complex Numbers

A complex number in standard form \( Z = a + j b \) may be written in exponential form as follows
\( \displaystyle Z = r e^{j \theta} \)      with \( j^2 = -1 \)
and in polar form as follows
\( Z = r \angle \theta \)
where \( r = \sqrt{a^2 +b^2} \) is the modulus of \( Z \) and \( \tan \theta = \dfrac{b}{a} \) its argument.
Take the real part, written as \( \Re e \) , of each side of a complex number in exponential form
\( \Re e (r e^{j \theta}) = \Re e (r ( \cos \theta + j \sin \theta )) = \Re e (r \cos \theta + j r \sin \theta ) = r \cos \theta \)
In what follows, \( \Re e \) means the real part of a given complex number.

B - Derivative of Complex Functions with One Variable

Let \( f(t) \) be a complex function with one variable \( t \) that is written of the form
\( f(t) = a(t) + j b(t) \)
where \( a(t) \) is the real part of \( f(t) \), \( b(t) \) is the imaginary part of \( f(t) \) and \( j = \sqrt {-1}\) is the imaginary unit.
Let \( f'(t) \) be the first derivative of \( f(t) \) with respect to \( t \) defined by
\( f'(t) = \lim_{h\to 0} \dfrac{f(t+h) - f(t) }{h} \)
Substitute \( f(t+h) \) by \( a(t+h) + j b(t+h) \) in the formula above.
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) + j b(t+h) - (a(t) + jb(t))}{h} \)
Separate terms as follows
\( f'(t) = \lim_{h\to 0} \dfrac{ a(t+h) - a(t)}{h} + j \lim_{h\to 0} \dfrac{ j b(t+h) - jb(t))}{h} \)
\( f'(t) = a'(t) + j b'(t) \)
It is now easy to show that the real part of the derivative of \( f(t) \) is equal to the derivative of the real part of \( f(t) \) which may be written as
\( \Re e(f'(t)) = a'(t) = (\Re e(f(t))' \)
or
\( \Re e \left ( \dfrac{df(t)}{dt} \right) = \dfrac {d a(t)}{dt} = \dfrac {d \left (\Re e(f(t)) \right)}{dt} \)

C - Integral of Complex Functions with One Variable

Let \( f(t) \) be a complex function with one variable \( t \) that is written of the form
\( f(t) = a(t) + j b(t) \)
where \( a(t) \) is the real part of \( f(t) \), \( b(t) \) is the imaginary part of \( f(t) \) and \( j = \sqrt {-1}\) is the imaginary unit.
Let \( F(t) \) be defined by indefinite integral
\( \displaystyle F(t) = \int f(t) dt = \int (a(t) + j b(t)) dt = \int a(t) dt + j \int b(t) dt \)
It is now easy to show that the real part of the indefinite of \( f(t) \) is equal to the indefinite integral of the real part of \( f(t) \) which may be written as
\( \displaystyle \Re e \left( \int f(t) dt \right) = \int a(t) dt = \int \left( \Re e f(t) \right) dt \)

We now use the above concepts to analyze simple AC circuits using complex numbers.

D - AC Voltage Source and Complex Numbers

In what follows, \( v(t) \) is an AC voltage source, that varies with time \( t \), given by
\( v(t) = V_0 \cos(\omega t) \)
where \( V_0 \) is a real number equal to the peak voltage and \( \omega = 2 \pi f \) is also a real number with \( f \) the frequency of the voltage source.
Using complex numbers, \( v(t) \) can also be written as
\( v(t) = V_0 \cos(\omega t) = \Re e ( V_0 \cos(\omega t) + j V_0 \sin(\omega t) ) = \Re e (V_0 e^{j\omega t} ) \)

E - Resistor in AC circuit

Let us consider a simple AC circuit with a resistor as shown below. Let \( v(t) \) be an AC voltage source given by
\( v(t) = V_0 \cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
where \( V_0 \) and \( \omega \) are real quantities.


The relationship between the current \( i \) through and the voltage \( v(t)_R \) across the resistor \( R \) is given by
\( v(t)_R = R i \)
Using the single loop shown above, we have
\( v(t) = v(t)_R \)
\( v(t) \) is given by \( v(t) = V_0 \cos(\omega t) \)
hence
\( v(t)_R = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
combining the above, we write
\( R i = \Re e (V_0 e^{j\omega t} ) \)       (I)
Let \( V_R = V_0 e^{j\omega t} \) and rewrite (I) above as
\( R i = \Re e V_R \)
since \( R \) is a real quantity, the above may be written as
\( i = \Re e \left( \dfrac{V_R }{R} \right) \)
Let \( Z_R \) be defined as the impedance of a resistor such that
\( Z_R = R \)
Since \( R \) is real, the impedance \( Z_R \) of a resistor is a real number.
Current \( i \) may then be written as
\( i = \Re e \left( \dfrac{ V_R } {Z_R} \right) \)
Let
\( I = \dfrac{ V_R } {Z_R} \)
The above gives a relationship similar to Ohm's law in DC (direct current) circuits. The above relationship between complex quantities \( I \), \( V_R \) and \( R \) makes calculations much easier.
This simplifies calculations in the sense that we do calculations using complex impedances, voltage and current and then take the real part as a final answer.

F - Capacitor in AC circuit

Let us consider a simple AC circuit with a capacitor as shown below. Let \( v(t) \) be an AC voltage source given by
\( v(t) = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

The relationship between the current \( i \) through and the voltage \( v(t)_C \) across the capacitor \( C \) is given by
\( \displaystyle v(t)_C = \dfrac{1}{C} \int i dt \)
Using the single loop shown above, we have
\( v(t) = v(t)_C \)
Given
\( v(t) = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
we combine all the above to write
\( \displaystyle \Re e (V_0 e^{j\omega t} ) = \dfrac{1}{C} \int i dt \)
Take the derivative of both sides
\( \displaystyle \dfrac{d}{dt} (\Re e (V_0 e^{j\omega t}) ) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
Use the above result discussed in part B above, we rewrite the above as
\( \displaystyle \Re e \dfrac{d}{dt} \left( V_0 e^{j\omega t} \right) = \dfrac{d}{dt} \left(\dfrac{1}{C} \int i dt \right) \)
Simplify
\( \Re e \left( j \omega V_0 e^{j\omega t} \right) = \dfrac{1}{C} i \)
Since the capacitance \( C \) is a real quantity, we can write
\( i = \Re e \left( j \omega C \; V_0 e^{j\omega t} \right) \)
Let \( V_C = V_0 e^{j\omega t} \) and define \( Z_C \) as the complex impedance of a capacitor such that
\( Z_C = \dfrac{1}{j \omega C} = - \dfrac {j} { \omega C} \)
Since \( C \) is real, the impedance \( Z_C \) of a capacitor is a pure imaginary number.
Current \( i \) may then be written as
\( i = \Re e \left( \dfrac{ V_C } {Z_C} \right) \)
Let
\( I = \dfrac{ V_C } {Z_C} \)
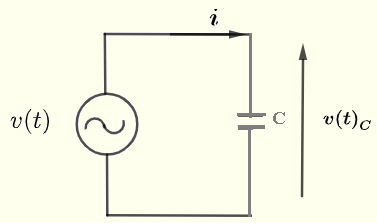
The above is similar to Ohm's law in DC (direct current) circuits. The above relationship between complex quantities \( I \), \( V_C \) and \( Z_C \) makes calculations much easier.
This simplifies calculations in the sense that we do calculations using complex impedances, voltage and current and then take the real part as a final answer.

G - Inductor in AC circuit

Let us consider a simple AC circuit with a capacitor as shown below. Let \( v(t) \) be an AC voltage source given by
\( v(t) = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)

The relationship between the current \( i \) through and the voltage \( v(t)_L \) across the inductor with inductance \( L \) is given by
\( v(t)_L = L \dfrac {d i}{ dt} \)
Using the single loop shown above, we have
\( v(t) = v(t)_L \)
Given
\( v(t) = V_0 cos(\omega t) = \Re e (V_0 e^{j\omega t} ) \)
we combine all the above to write
\( \Re e (V_0 e^{j\omega t} ) = L \dfrac {d i}{ dt} \)
Take the indefinite integral of both sides
\( \displaystyle \int \Re e (V_0 e^{j\omega t}) dt = \int L \dfrac {d i}{ dt} dt \)
Use the result already discussed in part C above, we rewrite the above as
\( \displaystyle \Re e \int V_0 e^{j\omega t} dt = \int L \dfrac {d i}{ dt} dt \)
Compute the integrals on both sides
\( \Re e \left( \dfrac{1}{j\omega} V_0 e^{j\omega t} \right) = L i \)
Since the inductance \( L \) is a real quantity, we can write
\( i = \Re e \left( \dfrac{1}{j \omega L} \; V_0 e^{j\omega t} \right) \)
Let \( V_L = V_0 e^{j\omega t} \) and \( Z_L \) be defined as the impedance of an inductor such that
\( Z_L = j \omega L \)
Since \( L \) is real, the impedance \( Z_L \) of a capacitor is a pure imaginary number.
The current \( i \) may then be written as
\( i = \Re e \left( \dfrac{ V_L } {Z_L} \right) \)
Let
\( I = \dfrac{ V_L } {Z_L} \)
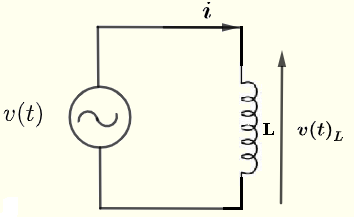
The above gives a relationship similar to Ohm's law between complex quantities \( I \), \( V_L \) and \( Z_L \).
This simplifies calculations in the sense that we do calculations using complex impedance, voltage and current and then take the real part as a final answer.

H - Conclusion: Ohm's Law with Complex Impedances

We have seen above that the impedances of resistors, capacitors and inductors may be defined as complex quantities which may be pure real or pure imaginary given by
1) For a resistor \( R\) ; the impedance is given by \[ Z_R = R \] and the relationship between the current \( I \) (in complex form) through and the voltage \( V_R \) (in complex form) across the resistor \( R \) is Ohm's law in AC and is given by: \[ I = \dfrac{V_R}{Z_R} \] 2) For a capacitor \( C \) ; the impedance is given by \[ Z_C = -\dfrac{j}{\omega C} \] and the relationship between the current \( I \) (in complex form) through and the voltage \( V_C \) (in complex form) across the capacitor \( C \) is Ohm's law in AC and is given by: \[ I = \dfrac{V_C}{Z_C} \] 3) For an inductor \( L \) ; the impedance is given by \[ Z_L = j \omega L \] and the relationship between the current \( I \) (in complex form) through and the voltage \( V_L \) (in complex form) across the inductor \( L \) is Ohm's law in AC and is given by: \[ I = \dfrac{V_C}{Z_L} \] We conclude that Ohm's law is valid in AC circuits when complex numbers are used to model impedances of resistors, capacitors and inductors.
It can also be shown that Kirchhoff's laws are also valid in AC circuits when complex numbers are used to model impedances of resistors, capacitors and inductors.
Equivalent impedances to series and parallel impedances may be computed using similar rules for series and parallel resistors.

E - Examples with Solutions

Example 1
Find the current \( i \), the voltage \( v(t)_R \) across the resistor \( R \) and the voltage \( v(t)_L \) across the inductor \( L \) in terms of \( V_0 \), \( R \), \( L \) and \( \omega \) given
voltage source: \( v(t) = V_0 cos(\omega t) \) , \( \omega = 2 \pi f \) and \( f \) is the frequency.

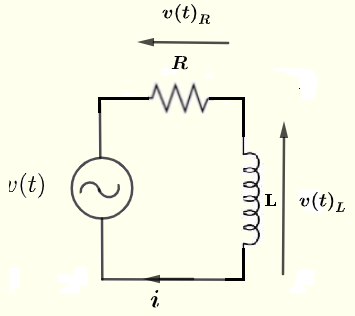
Solution to Example 1
Let \( V \) be the complex form of the voltage source \( v(t) \).
Let \( V_R \) be the complex form of the voltage \( v(t)_R\) across the resistor R.
Let \( V_L \) be the complex form of the voltage \( v(t)_L\) across the inductor L
Let \( I \) the complex form of the current \( i \) through the resistor and the capacitor in the given circuit.
Let the complex impedance of a resistor to be \( Z_R = R \) and that of the inductor to be \(Z_L = j \omega L \) (see part H above).
Redraw the circuit with the complex quantities defined above and you may apply Ohm's and Kirchhoff's laws.

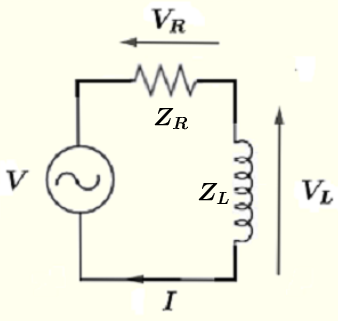
Using Kirchhoff's law on the loop making the circuit, we have
\( V = V_R + V_L \)         (I)
Using Ohm's law to rewrite \( V_R \) and \( V_L \) as
\( V_R = Z_R I \)
\( V_L = Z_L I \)
Substitute in equation (I)
\( V = Z_R I + Z_L I = R I + j \omega L I = I(R + j \omega L ) \)
Solve the above for \( I \)
\( I = \dfrac{V}{R+j \omega L} \)         (II)
The denominator \( R+j \omega L \) is a complex number that may be written in complex form as
\( R+j \omega L = r e^{j\theta} \)
where
\( r = |Z| = \sqrt {R^2 + (L\omega)^2} \) is the modulus
\( \theta = \arctan \left(\dfrac{\omega L}{R} \right) \) is the argument as shown in the complex plane below.

Let \( V = V_0 e^{j\omega t} \)
Substitute \( V \) and \( R+j \omega L \) by their complex forms in (II) and write
\( I = \dfrac{V_0 e^{j\omega t}}{r e^{j\theta}} \)
Use exponential rules to simplify the above
\( I = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Use Ohm's law to write
\( V_R = R I = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)

\( V_L = Z_L I = \dfrac{j V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Write \( j \) in exponential form \( j = e^{j \pi/2} \)in \( V_L \)
\( V_L = \dfrac{ e^{j \pi/2} V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \)
Use exponential rule to rewrite the above as
\( V_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \)
We now use the complex quantities computed above to compute \( i \), \( v(t)_R \) and \( v(t)_L \) by taking the real parts as follows:
\( i = \Re e I = \Re e \left( \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \)
which gives
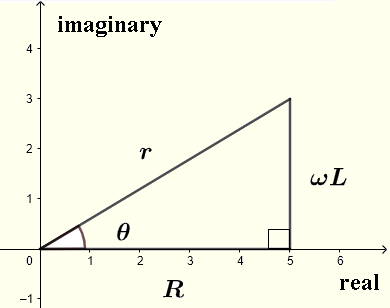
\[ i = \dfrac{V_0}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_R = \Re e V_R = \Re e \left( \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t-\theta)} \right) \) \[ v(t)_R = \dfrac{V_0 R}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t-\theta) \] \( v(t)_L = \Re e V_L = \Re e \left( \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} e^{j(\omega t + \pi/2 -\theta)} \right) \) \[ v(t)_L = \dfrac{V_0 \omega L}{\sqrt{R^2 + (L\omega)^2}} \cos (\omega t + \pi/2 -\theta) \]

More References and Links