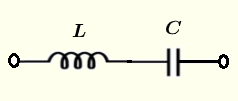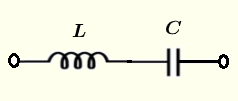Series LC circuit Impedance Calculator
Table of Contents
A calculator to calculate the equivalent impedance of an inductor and a capacitor in series.
Complex numbers in standard form and
polar forms are used in the calculations and the presentation of the results.
\( \) \( \) \( \)
Formulae for Series LC Circuit Impedance Used in Calculator and their Units
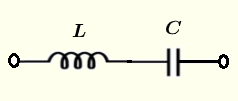
Let \( f \) be the frequency, in Hertz, of the source voltage supplying the circuit.
and define the following parameters used in the calculations
\( \omega = 2 \pi f \) , angular frequency in rad/s
\( X_L = \omega L \) , the inductive reactance in ohms \( (\Omega) \)
The impedance of the inductor \( L \) is given by
\( Z_L = j \omega L \)
\( X_C = 1 / (\omega C) \) , the capacitive reactance in ohms \( (\Omega) \)
The impedance of the capacitor \( C \) is given by
\( Z_C = \dfrac{1}{j \omega C} = -\dfrac{j}{\omega C}\)
Let \( Z \) be the equivalent impedance to the series LC circuit shown above and write it in complex form as follows
\[ Z = Z_L + Z_C = j\omega L - \dfrac{j}{\omega C} = j \left(\omega L - \dfrac{1}{\omega C} \right) \]
The formulae for the modulus \( |Z| \) and argument (or phase) \( \theta \) of \( Z \) are given by
Modulus: \( |Z| = \left| \omega L - \dfrac{1}{\omega C} \right| \)
Argument (Phase): \( \theta = \dfrac{\pi}{2} \) or \( 90^{\circ} \) if \( \omega L \gt \dfrac{1}{\omega C} \)
Argument (Phase): \( \theta = - \dfrac{\pi}{2} \) or \( - 90^{\circ} \) if \( \omega L \lt \dfrac{1}{\omega C} \)
Argument (Phase): \( \theta = 0 \) if \( \omega L = \dfrac{1}{\omega C} \)
Use of the calculator
Enter the resistance, the capacitance and the frequency as positive real numbers with the given units then press "calculate".
Results of Calculations
More References and links
AC Circuits Calculators and Solvers
Complex Numbers - Basic Operations
Complex Numbers in Exponential Form
Complex Numbers in Polar Form
Convert a Complex Number to Polar and Exponential Forms Calculator
Engineering Mathematics with Examples and Solutions